Detecting Causality in the Frequency Domain with Cross-Mapping Coherence

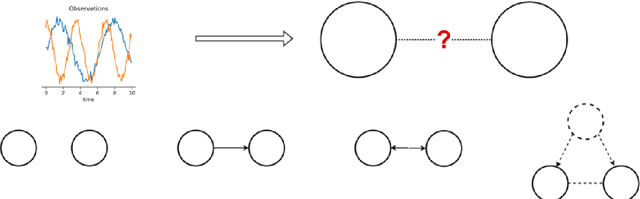
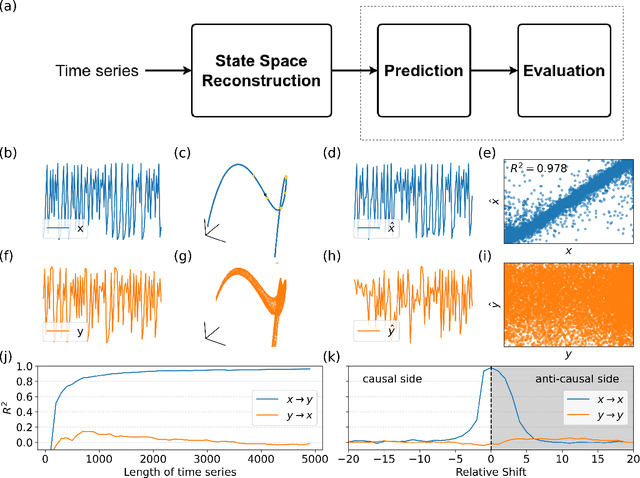
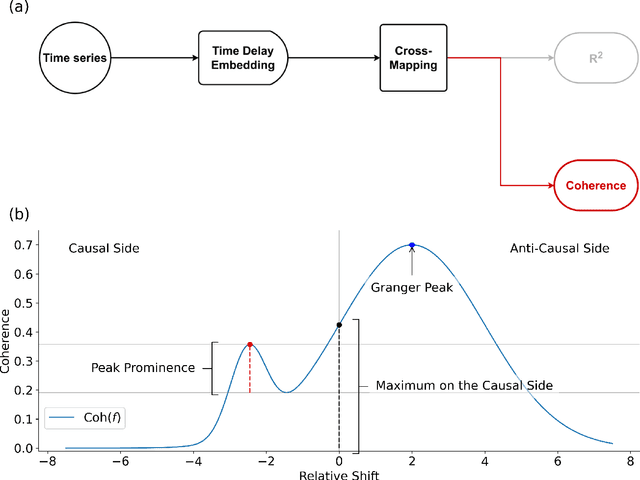
Understanding causal relationships within a system is crucial for uncovering its underlying mechanisms. Causal discovery methods, which facilitate the construction of such models from time-series data, hold the potential to significantly advance scientific and engineering fields. This study introduces the Cross-Mapping Coherence (CMC) method, designed to reveal causal connections in the frequency domain between time series. CMC builds upon nonlinear state-space reconstruction and extends the Convergent Cross-Mapping algorithm to the frequency domain by utilizing coherence metrics for evaluation. We tested the Cross-Mapping Coherence method using simulations of logistic maps, Lorenz systems, Kuramoto oscillators, and the Wilson-Cowan model of the visual cortex. CMC accurately identified the direction of causal connections in all simulated scenarios. When applied to the Wilson-Cowan model, CMC yielded consistent results similar to spectral Granger causality. Furthermore, CMC exhibits high sensitivity in detecting weak connections, demonstrates sample efficiency, and maintains robustness in the presence of noise. In conclusion, the capability to determine directed causal influences across different frequency bands allows CMC to provide valuable insights into the dynamics of complex, nonlinear systems.

Reconstructing common latent input from time series with the mapper-coach network and error backpropagation

A two-module, feedforward neural network architecture called mapper-coach network has been introduced to reconstruct an unobserved, continuous latent variable input, driving two observed dynamical systems. The method has been demonstrated on time series generated by two chaotic logistic maps driven by a hidden third one. The network has been trained to predict one of the observed time series based on its own past and on the other observed time series by error-back propagation. It was shown, that after this prediction have been learned successfully, the activity of the bottleneck neuron, connecting the mapper and the coach module, correlates strongly with the latent common input variable. The method has the potential to reveal hidden components of dynamical systems, where experimental intervention is not possible.

Manifold-adaptive dimension estimation revisited

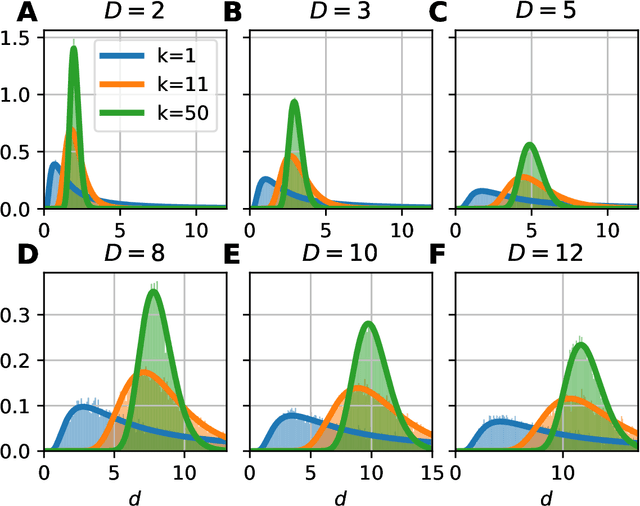
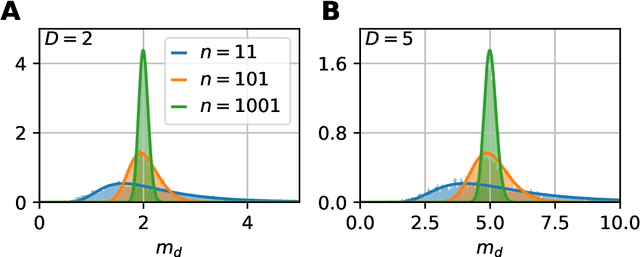
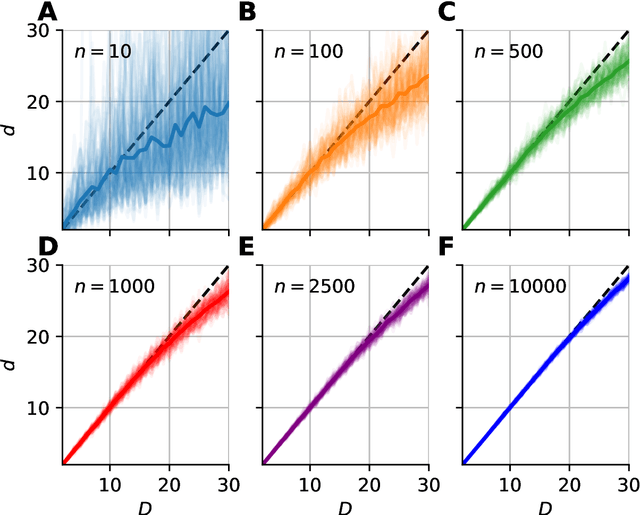
Data dimensionality informs us about data complexity and sets limit on the structure of successful signal processing pipelines. In this work we revisit and improve the manifold-adaptive Farahmand-Szepesv\'ari-Audibert (FSA) dimension estimator, making it one of the best nearest neighbor-based dimension estimators available. We compute the probability density function of local FSA estimates, if the local manifold density is uniform. Based on the probability density function, we propose to use the median of local estimates as a basic global measure of intrinsic dimensionality, and we demonstrate the advantages of this asymptotically unbiased estimator over the previously proposed statistics: the mode and the mean. Additionally, from the probability density function, we derive the maximum likelihood formula for global intrinsic dimensionality, if i.i.d. holds. We tackle edge and finite-sample effects with an exponential correction formula, calibrated on hypercube datasets. We compare the performance of the corrected-median-FSA estimator with kNN estimators: maximum likelihood (ML, Levina-Bickel) and two implementations of DANCo (R and matlab). We show that corrected-median-FSA estimator beats the ML estimator and it is on equal footing with DANCo for standard synthetic benchmarks according to mean percentage error and error rate metrics. With the median-FSA algorithm, we reveal diverse changes in the neural dynamics while resting state and during epileptic seizures. We identify brain areas with lower-dimensional dynamics that are possible causal sources and candidates for being seizure onset zones.

How to find a unicorn: a novel model-free, unsupervised anomaly detection method for time series

Recognition of anomalous events is a challenging but critical task in many scientific and industrial fields, especially when the properties of anomalies are unknown. In this paper, we present a new anomaly concept called "unicorn" or unique event and present a new, model-independent, unsupervised detection algorithm to detect unicorns. The Temporal Outlier Factor (TOF) is introduced to measure the uniqueness of events in continuous data sets from dynamic systems. The concept of unique events differs significantly from traditional outliers in many aspects: while repetitive outliers are no longer unique events, a unique event is not necessarily outlier in either pointwise or collective sense; it does not necessarily fall out from the distribution of normal activity. The performance of our algorithm was examined in recognizing unique events on different types of simulated data sets with anomalies and it was compared with the standard Local Outlier Factor (LOF). TOF had superior performance compared to LOF even in recognizing traditional outliers and it also recognized unique events that LOF did not. Benefits of the unicorn concept and the new detection method were illustrated by example data sets from very different scientific fields. Our algorithm successfully recognized unique events in those cases where they were already known such as the gravitational waves of a black hole merger on LIGO detector data and the signs of respiratory failure on ECG data series. Furthermore, unique events were found on the LIBOR data set of the last 30 years.