Manifold-adaptive dimension estimation revisited
Paper and Code
Aug 10, 2020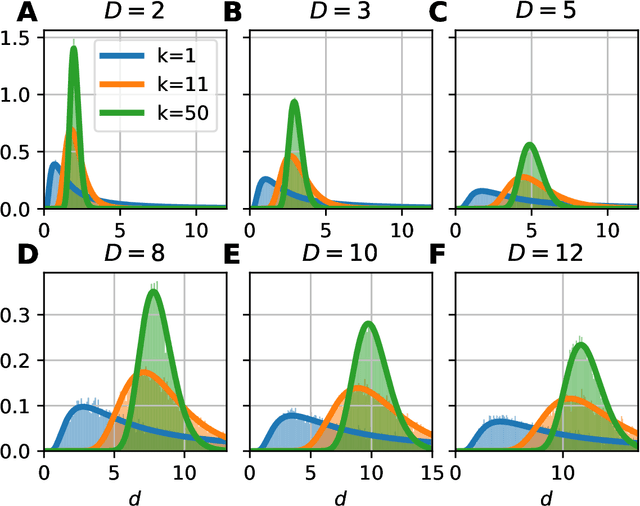
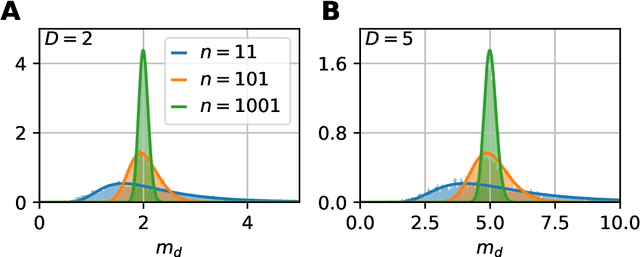
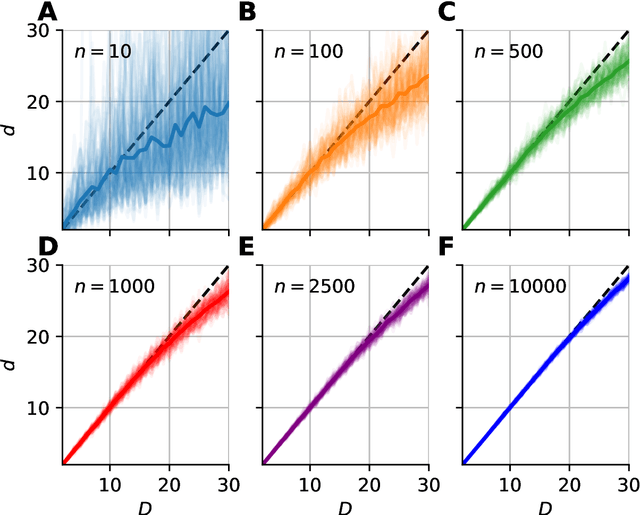

Data dimensionality informs us about data complexity and sets limit on the structure of successful signal processing pipelines. In this work we revisit and improve the manifold-adaptive Farahmand-Szepesv\'ari-Audibert (FSA) dimension estimator, making it one of the best nearest neighbor-based dimension estimators available. We compute the probability density function of local FSA estimates, if the local manifold density is uniform. Based on the probability density function, we propose to use the median of local estimates as a basic global measure of intrinsic dimensionality, and we demonstrate the advantages of this asymptotically unbiased estimator over the previously proposed statistics: the mode and the mean. Additionally, from the probability density function, we derive the maximum likelihood formula for global intrinsic dimensionality, if i.i.d. holds. We tackle edge and finite-sample effects with an exponential correction formula, calibrated on hypercube datasets. We compare the performance of the corrected-median-FSA estimator with kNN estimators: maximum likelihood (ML, Levina-Bickel) and two implementations of DANCo (R and matlab). We show that corrected-median-FSA estimator beats the ML estimator and it is on equal footing with DANCo for standard synthetic benchmarks according to mean percentage error and error rate metrics. With the median-FSA algorithm, we reveal diverse changes in the neural dynamics while resting state and during epileptic seizures. We identify brain areas with lower-dimensional dynamics that are possible causal sources and candidates for being seizure onset zones.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge