A physics-driven sensor placement optimization methodology for temperature field reconstruction

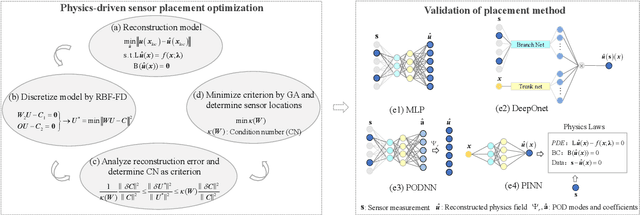
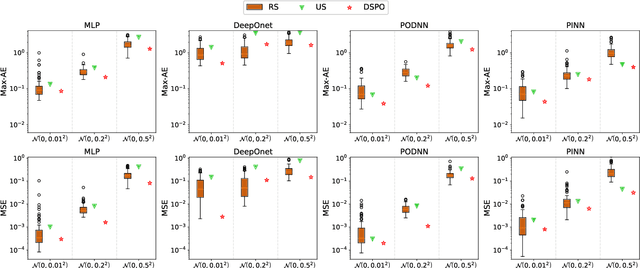
Perceiving the global field from sparse sensors has been a grand challenge in the monitoring, analysis, and design of physical systems. In this context, sensor placement optimization is a crucial issue. Most existing works require large and sufficient data to construct data-based criteria, which are intractable in data-free scenarios without numerical and experimental data. To this end, we propose a novel physics-driven sensor placement optimization (PSPO) method for temperature field reconstruction using a physics-based criterion to optimize sensor locations. In our methodological framework, we firstly derive the theoretical upper and lower bounds of the reconstruction error under noise scenarios by analyzing the optimal solution, proving that error bounds correlate with the condition number determined by sensor locations. Furthermore, the condition number, as the physics-based criterion, is used to optimize sensor locations by the genetic algorithm. Finally, the best sensors are validated by reconstruction models, including non-invasive end-to-end models, non-invasive reduced-order models, and physics-informed models. Experimental results, both on a numerical and an application case, demonstrate that the PSPO method significantly outperforms random and uniform selection methods, improving the reconstruction accuracy by nearly an order of magnitude. Moreover, the PSPO method can achieve comparable reconstruction accuracy to the existing data-driven placement optimization methods.

RBF-MGN:Solving spatiotemporal PDEs with Physics-informed Graph Neural Network

Physics-informed neural networks (PINNs) have lately received significant attention as a representative deep learning-based technique for solving partial differential equations (PDEs). Most fully connected network-based PINNs use automatic differentiation to construct loss functions that suffer from slow convergence and difficult boundary enforcement. In addition, although convolutional neural network (CNN)-based PINNs can significantly improve training efficiency, CNNs have difficulty in dealing with irregular geometries with unstructured meshes. Therefore, we propose a novel framework based on graph neural networks (GNNs) and radial basis function finite difference (RBF-FD). We introduce GNNs into physics-informed learning to better handle irregular domains with unstructured meshes. RBF-FD is used to construct a high-precision difference format of the differential equations to guide model training. Finally, we perform numerical experiments on Poisson and wave equations on irregular domains. We illustrate the generalizability, accuracy, and efficiency of the proposed algorithms on different PDE parameters, numbers of collection points, and several types of RBFs.