Learning-Based Pricing and Matching for Two-Sided Queues

We consider a dynamic system with multiple types of customers and servers. Each type of waiting customer or server joins a separate queue, forming a bipartite graph with customer-side queues and server-side queues. The platform can match the servers and customers if their types are compatible. The matched pairs then leave the system. The platform will charge a customer a price according to their type when they arrive and will pay a server a price according to their type. The arrival rate of each queue is determined by the price according to some unknown demand or supply functions. Our goal is to design pricing and matching algorithms to maximize the profit of the platform with unknown demand and supply functions, while keeping queue lengths of both customers and servers below a predetermined threshold. This system can be used to model two-sided markets such as ride-sharing markets with passengers and drivers. The difficulties of the problem include simultaneous learning and decision making, and the tradeoff between maximizing profit and minimizing queue length. We use a longest-queue-first matching algorithm and propose a learning-based pricing algorithm, which combines gradient-free stochastic projected gradient ascent with bisection search. We prove that our proposed algorithm yields a sublinear regret $\tilde{O}(T^{5/6})$ and queue-length bound $\tilde{O}(T^{2/3})$, where $T$ is the time horizon. We further establish a tradeoff between the regret bound and the queue-length bound: $\tilde{O}(T^{1-\gamma/4})$ versus $\tilde{O}(T^{\gamma})$ for $\gamma \in (0, 2/3].$

Online Nonstochastic Control with Adversarial and Static Constraints

This paper studies online nonstochastic control problems with adversarial and static constraints. We propose online nonstochastic control algorithms that achieve both sublinear regret and sublinear adversarial constraint violation while keeping static constraint violation minimal against the optimal constrained linear control policy in hindsight. To establish the results, we introduce an online convex optimization with memory framework under adversarial and static constraints, which serves as a subroutine for the constrained online nonstochastic control algorithms. This subroutine also achieves the state-of-the-art regret and constraint violation bounds for constrained online convex optimization problems, which is of independent interest. Our experiments demonstrate the proposed control algorithms are adaptive to adversarial constraints and achieve smaller cumulative costs and violations. Moreover, our algorithms are less conservative and achieve significantly smaller cumulative costs than the state-of-the-art algorithm.

MaxWeight With Discounted UCB: A Provably Stable Scheduling Policy for Nonstationary Multi-Server Systems With Unknown Statistics

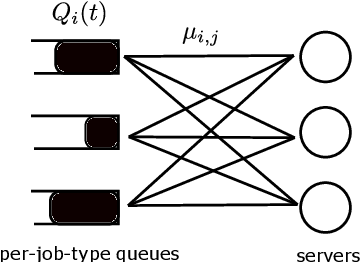
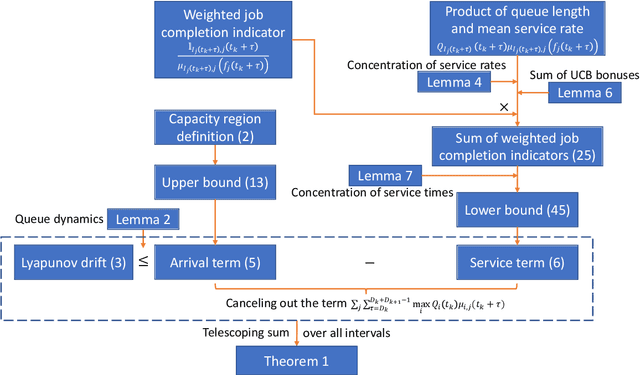
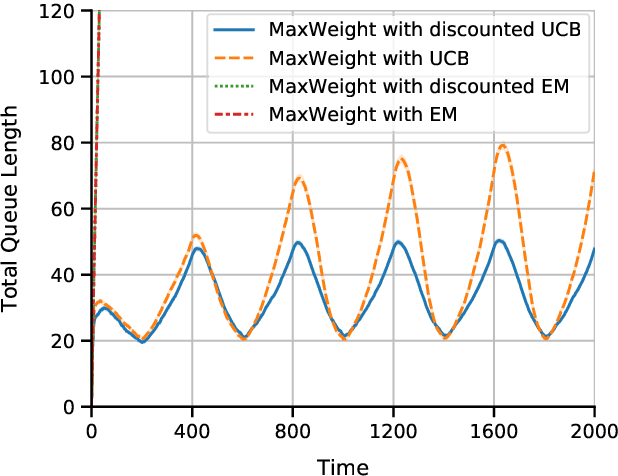
Multi-server queueing systems are widely used models for job scheduling in machine learning, wireless networks, and crowdsourcing. This paper considers a multi-server system with multiple servers and multiple types of jobs. The system maintains a separate queue for each type of jobs. For each time slot, each available server picks a job from a queue and then serves the job until it is complete. The arrival rates of the queues and the mean service times are unknown and even nonstationary. We propose the MaxWeight with discounted upper confidence bound (UCB) algorithm, which simultaneously learns the statistics and schedules jobs to servers. We prove that the proposed algorithm can stabilize the queues when the arrival rates are strictly within the service capacity region. Specifically, we prove that the queue lengths are bounded in the mean under the assumption that the mean service times change relatively slowly over time and the arrival rates are bounded away from the capacity region by a constant whose value depends on the discount factor used in the discounted UCB. Simulation results confirm that the proposed algorithm can stabilize the queues and that it outperforms MaxWeight with empirical mean and MaxWeight with discounted empirical mean. The proposed algorithm is also better than MaxWeight with UCB in the nonstationary setting.

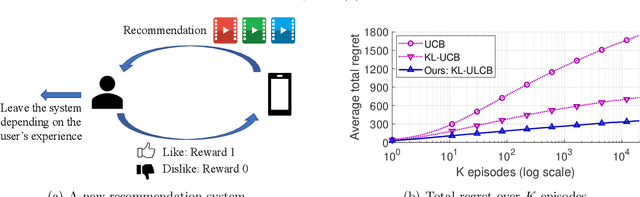
Exploration, Exploitation, and Engagement in Multi-Armed Bandits with Abandonment

Multi-armed bandit (MAB) is a classic model for understanding the exploration-exploitation trade-off. The traditional MAB model for recommendation systems assumes the user stays in the system for the entire learning horizon. In new online education platforms such as ALEKS or new video recommendation systems such as TikTok and YouTube Shorts, the amount of time a user spends on the app depends on how engaging the recommended contents are. Users may temporarily leave the system if the recommended items cannot engage the users. To understand the exploration, exploitation, and engagement in these systems, we propose a new model, called MAB-A where "A" stands for abandonment and the abandonment probability depends on the current recommended item and the user's past experience (called state). We propose two algorithms, ULCB and KL-ULCB, both of which do more exploration (being optimistic) when the user likes the previous recommended item and less exploration (being pessimistic) when the user does not like the previous item. We prove that both ULCB and KL-ULCB achieve logarithmic regret, $O(\log K)$, where $K$ is the number of visits (or episodes). Furthermore, the regret bound under KL-ULCB is asymptotically sharp. We also extend the proposed algorithms to the general-state setting. Simulation results confirm our theoretical analysis and show that the proposed algorithms have significantly lower regrets than the traditional UCB and KL-UCB, and Q-learning-based algorithms.