MaxWeight With Discounted UCB: A Provably Stable Scheduling Policy for Nonstationary Multi-Server Systems With Unknown Statistics
Paper and Code
Sep 02, 2022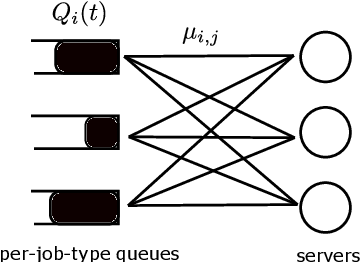
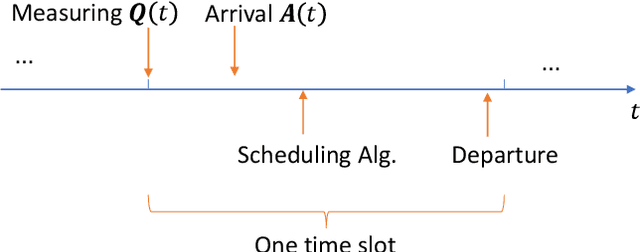
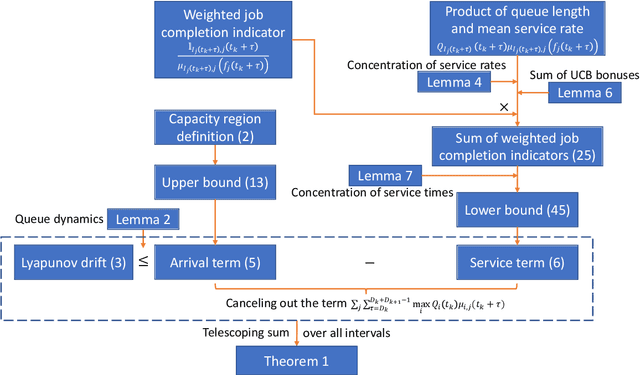
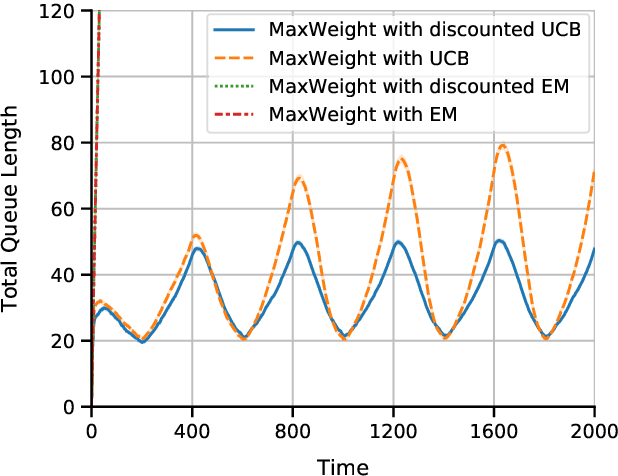
Multi-server queueing systems are widely used models for job scheduling in machine learning, wireless networks, and crowdsourcing. This paper considers a multi-server system with multiple servers and multiple types of jobs. The system maintains a separate queue for each type of jobs. For each time slot, each available server picks a job from a queue and then serves the job until it is complete. The arrival rates of the queues and the mean service times are unknown and even nonstationary. We propose the MaxWeight with discounted upper confidence bound (UCB) algorithm, which simultaneously learns the statistics and schedules jobs to servers. We prove that the proposed algorithm can stabilize the queues when the arrival rates are strictly within the service capacity region. Specifically, we prove that the queue lengths are bounded in the mean under the assumption that the mean service times change relatively slowly over time and the arrival rates are bounded away from the capacity region by a constant whose value depends on the discount factor used in the discounted UCB. Simulation results confirm that the proposed algorithm can stabilize the queues and that it outperforms MaxWeight with empirical mean and MaxWeight with discounted empirical mean. The proposed algorithm is also better than MaxWeight with UCB in the nonstationary setting.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge