Efficient Neural Hybrid System Learning and Transition System Abstraction for Dynamical Systems

This paper proposes a neural network hybrid modeling framework for dynamics learning to promote an interpretable, computationally efficient way of dynamics learning and system identification. First, a low-level model will be trained to learn the system dynamics, which utilizes multiple simple neural networks to approximate the local dynamics generated from data-driven partitions. Then, based on the low-level model, a high-level model will be trained to abstract the low-level neural hybrid system model into a transition system that allows Computational Tree Logic Verification to promote the model's ability with human interaction and verification efficiency.

A Transition System Abstraction Framework for Neural Network Dynamical System Models

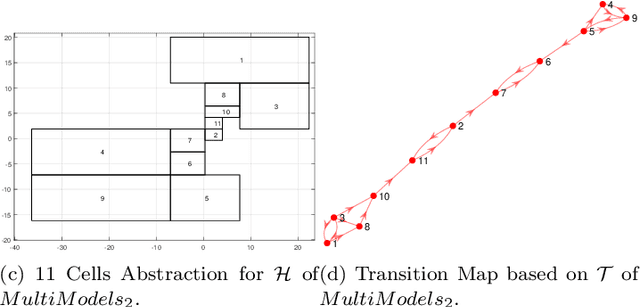
This paper proposes a transition system abstraction framework for neural network dynamical system models to enhance the model interpretability, with applications to complex dynamical systems such as human behavior learning and verification. To begin with, the localized working zone will be segmented into multiple localized partitions under the data-driven Maximum Entropy (ME) partitioning method. Then, the transition matrix will be obtained based on the set-valued reachability analysis of neural networks. Finally, applications to human handwriting dynamics learning and verification are given to validate our proposed abstraction framework, which demonstrates the advantages of enhancing the interpretability of the black-box model, i.e., our proposed framework is able to abstract a data-driven neural network model into a transition system, making the neural network model interpretable through verifying specifications described in Computational Tree Logic (CTL) languages.

Compression Repair for Feedforward Neural Networks Based on Model Equivalence Evaluation

In this paper, we propose a method of repairing compressed Feedforward Neural Networks (FNNs) based on equivalence evaluation of two neural networks. In the repairing framework, a novel neural network equivalence evaluation method is developed to compute the output discrepancy between two neural networks. The output discrepancy can quantitatively characterize the output difference produced by compression procedures. Based on the computed output discrepancy, the repairing method first initializes a new training set for the compressed networks to narrow down the discrepancy between the two neural networks and improve the performance of the compressed network. Then, we repair the compressed FNN by re-training based on the training set. We apply our developed method to the MNIST dataset to demonstrate the effectiveness and advantages of our proposed repair method.

Guaranteed Quantization Error Computation for Neural Network Model Compression

Neural network model compression techniques can address the computation issue of deep neural networks on embedded devices in industrial systems. The guaranteed output error computation problem for neural network compression with quantization is addressed in this paper. A merged neural network is built from a feedforward neural network and its quantized version to produce the exact output difference between two neural networks. Then, optimization-based methods and reachability analysis methods are applied to the merged neural network to compute the guaranteed quantization error. Finally, a numerical example is proposed to validate the applicability and effectiveness of the proposed approach.

A Data-Driven Hybrid Automaton Framework to Modeling Complex Dynamical Systems

In this paper, a computationally efficient data-driven hybrid automaton model is proposed to capture unknown complex dynamical system behaviors using multiple neural networks. The sampled data of the system is divided by valid partitions into groups corresponding to their topologies and based on which, transition guards are defined. Then, a collection of small-scale neural networks that are computationally efficient are trained as the local dynamical description for their corresponding topologies. After modeling the system with a neural-network-based hybrid automaton, the set-valued reachability analysis with low computation cost is provided based on interval analysis and a split and combined process. At last, a numerical example of the limit cycle is presented to illustrate that the developed models can significantly reduce the computational cost in reachable set computation without sacrificing any modeling precision.