Zhongwen Sun
Performance Analysis of Wireless Network Aided by Discrete-Phase-Shifter IRS
Apr 13, 2022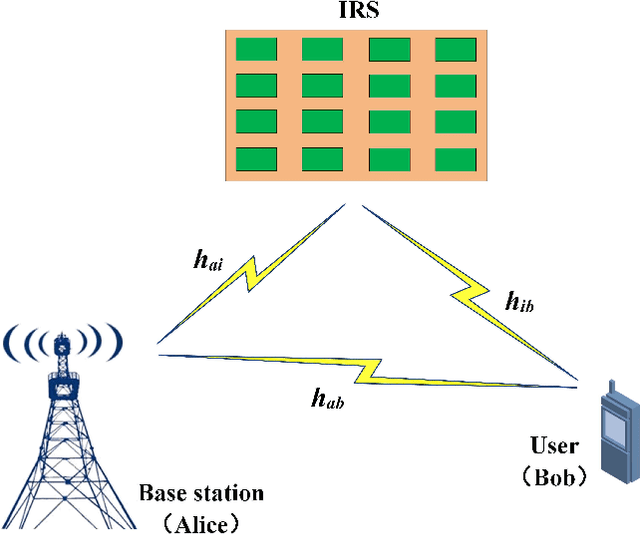
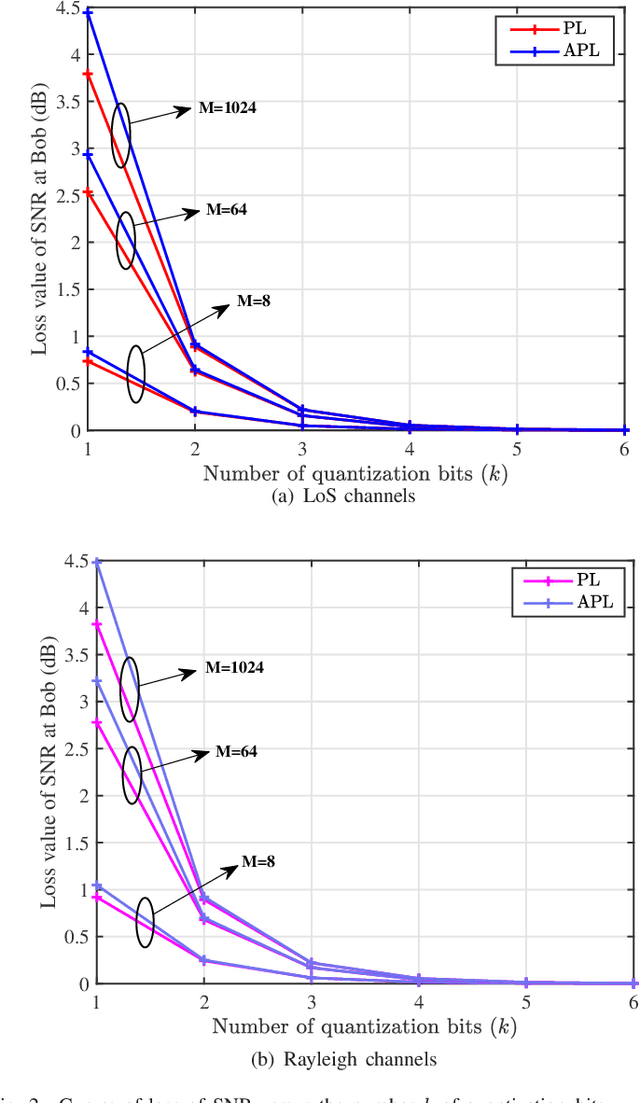
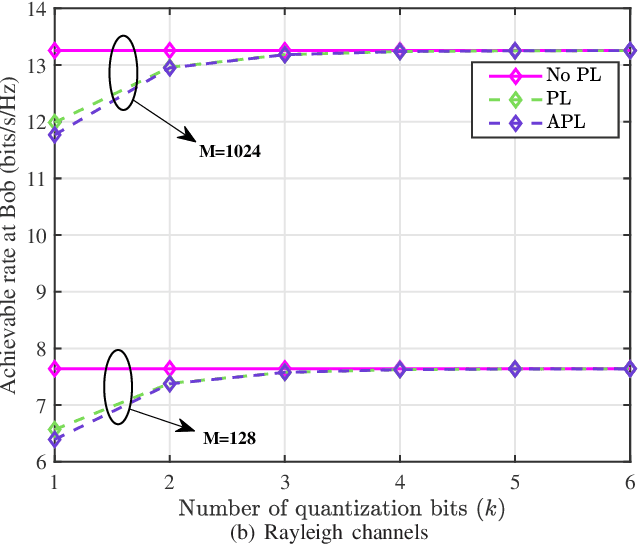
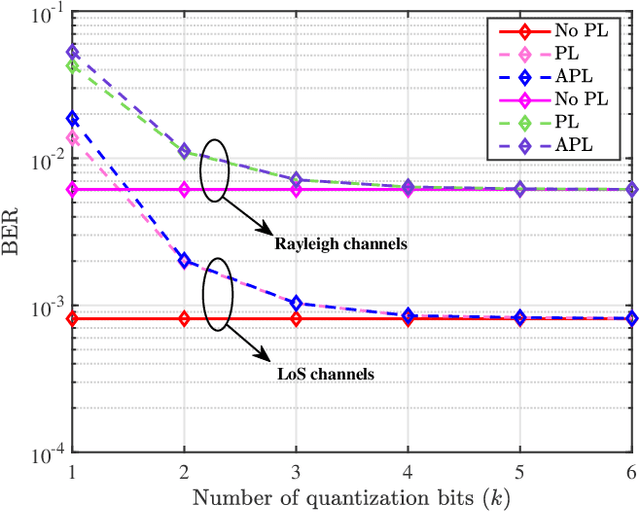
Abstract:Discrete phase shifters of intelligent reflecting surface (IRS) generates phase quantization error (QE) and degrades the receive performance at the receiver. To make an analysis of the performance loss caused by IRS with phase QE, based on the law of large numbers, the closed-form expressions of signal-to-noise ratio (SNR) performance loss (PL), achievable rate (AR), and bit error rate (BER) are successively derived under line-of-sight (LoS) channels and Rayleigh channels. Moreover, based on the Taylor series expansion, the approximate simple closed form of PL of IRS with approximate QE is also given. The simulation results show that the performance losses of SNR and AR decrease as the number of quantization bits increase, while they gradually increase with the number of IRS phase shifter elements increase. Regardless of LoS channels or Rayleigh channels, when the number of quantization bits is larger than or equal to 3, the performance losses of SNR and AR are less than 0.23dB and 0.08bits/s/Hz, respectively, and the BER performance degradation is trivial. In particular, the performance loss difference between IRS with QE and IRS with approximate QE is negligible when the number of quantization bits is not less than 2.
Pilot Optimization and Channel Estimation for Two-way Relaying Network Aided by IRS with Finite Discrete Phase Shifters
Oct 28, 2021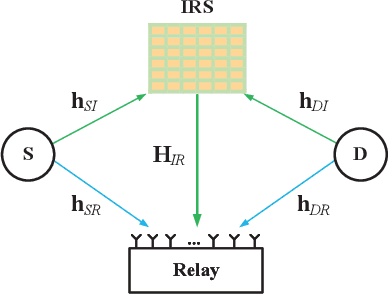
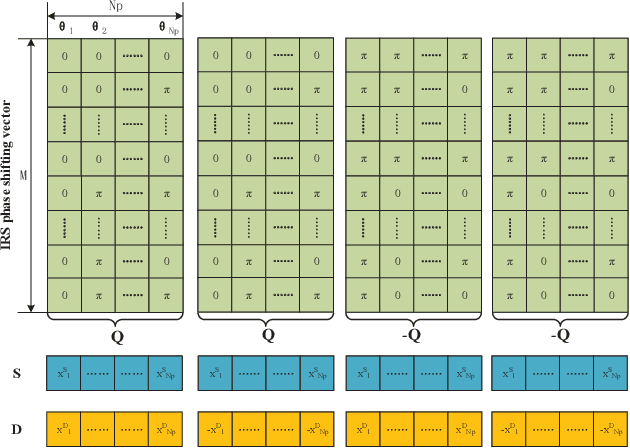
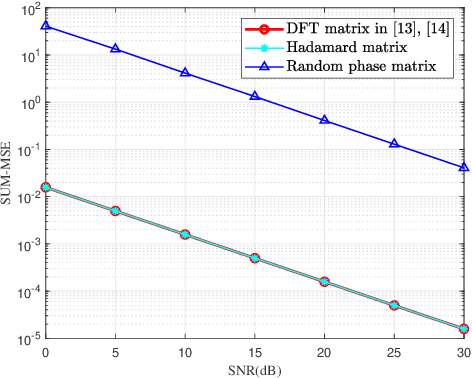
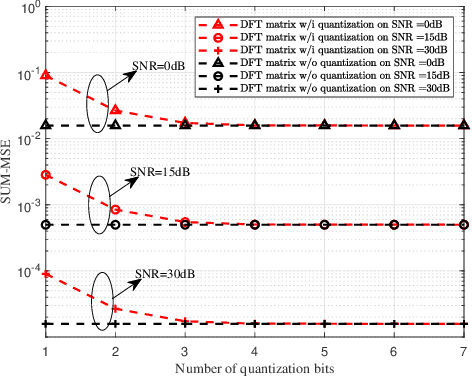
Abstract:In this paper, we investigate the problem of pilot optimization and channel estimation of two-way relaying network (TWRN) aided by an intelligent reflecting surface (IRS) with finite discrete phase shifters. In a TWRN, there exists a challenging problem that the two cascading channels from source-to-IRS-to-Relay and destination-to-IRS-to-relay interfere with each other. Via designing the initial phase shifts of IRS and pilot pattern, the two cascading channels are separated by using simple arithmetic operations like addition and subtraction. Then, the least-squares estimator is adopted to estimate the two cascading channels and two direct channels from source to relay and destination to relay. The corresponding mean square errors (MSE) of channel estimators are derived. By minimizing MSE, the optimal phase shift matrix of IRS is proved. Then, two special matrices Hadamard and discrete Fourier transform (DFT) matrix is shown to be two optimal training matrices for IRS. Furthermore, the IRS with discrete finite phase shifters is taken into account. Using theoretical derivation and numerical simulations, we find that 3-4 bits phase shifters are sufficient for IRS to achieve a negligible MSE performance loss. More importantly, the Hadamard matrix requires only one-bit phase shifters to achieve the optimal MSE performance while the DFT matrix requires at least three or four bits to achieve the same performance. Thus, the Hadamard matrix is a perfect choice for channel estimation using low-resolution phase-shifting IRS.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge