Zhihang Yin
Dynamic Programming-Based Redundancy Resolution for Path Planning of Redundant Manipulators Considering Breakpoints
Nov 26, 2024Abstract:This paper proposes a redundancy resolution algorithm for a redundant manipulator based on dynamic programming. This algorithm can compute the desired joint angles at each point on a pre-planned discrete path in Cartesian space, while ensuring that the angles, velocities, and accelerations of each joint do not exceed the manipulator's constraints. We obtain the analytical solution to the inverse kinematics problem of the manipulator using a parameterization method, transforming the redundancy resolution problem into an optimization problem of determining the parameters at each path point. The constraints on joint velocity and acceleration serve as constraints for the optimization problem. Then all feasible inverse kinematic solutions for each pose under the joint angle constraints of the manipulator are obtained through parameterization methods, and the globally optimal solution to this problem is obtained through the dynamic programming algorithm. On the other hand, if a feasible joint-space path satisfying the constraints does not exist, the proposed algorithm can compute the minimum number of breakpoints required for the path and partition the path with as few breakpoints as possible to facilitate the manipulator's operation along the path. The algorithm can also determine the optimal selection of breakpoints to minimize the global cost function, rather than simply interrupting when the manipulator is unable to continue operating. The proposed algorithm is tested using a manipulator produced by a certain manufacturer, demonstrating the effectiveness of the algorithm.
Dynamic Programming-Based Offline Redundancy Resolution of Redundant Manipulators Along Prescribed Paths with Real-Time Adjustment
Nov 26, 2024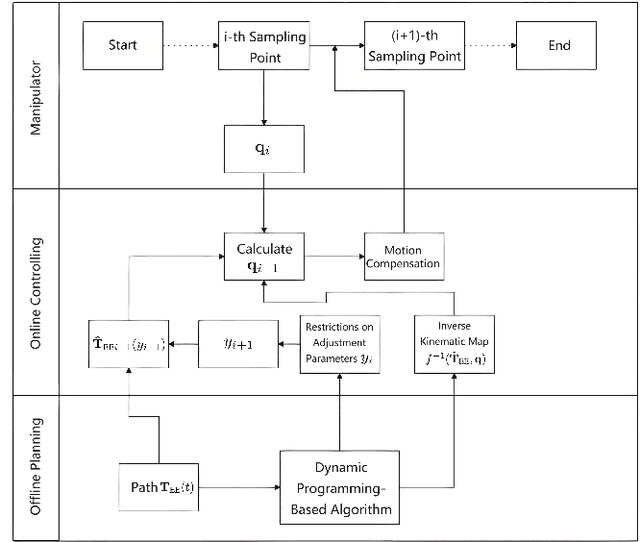
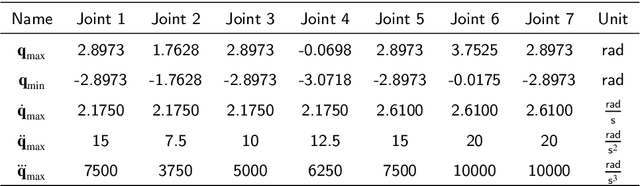
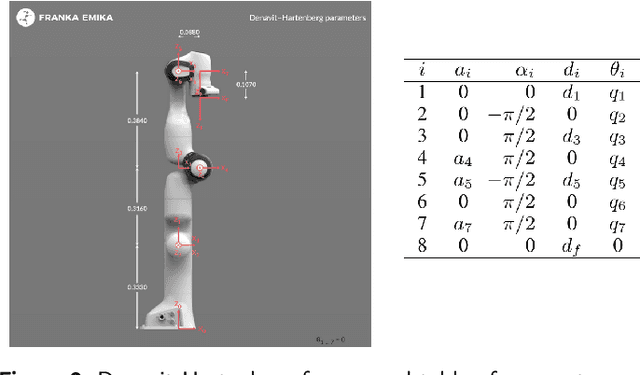
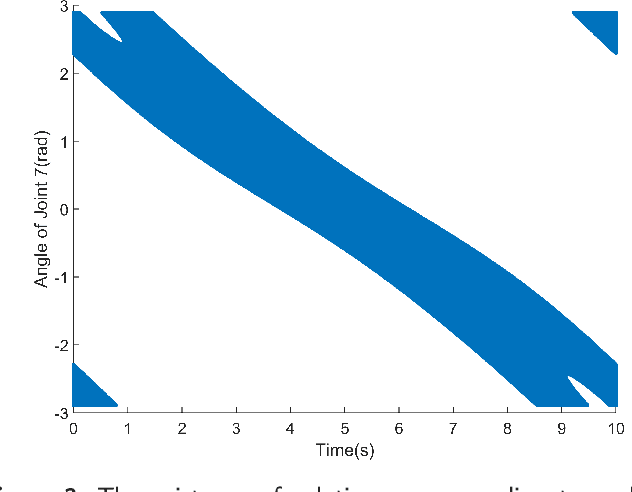
Abstract:Traditional offline redundancy resolution of trajectories for redundant manipulators involves computing inverse kinematic solutions for Cartesian space paths, constraining the manipulator to a fixed path without real-time adjustments. Online redundancy resolution can achieve real-time adjustment of paths, but it cannot consider subsequent path points, leading to the possibility of the manipulator being forced to stop mid-motion due to joint constraints. To address this, this paper introduces a dynamic programming-based offline redundancy resolution for redundant manipulators along prescribed paths with real-time adjustment. The proposed method allows the manipulator to move along a prescribed path while implementing real-time adjustment along the normal to the path. Using Dynamic Programming, the proposed approach computes a global maximum for the variation of adjustment coefficients. As long as the coefficient variation between adjacent sampling path points does not exceed this limit, the algorithm provides the next path point's joint angles based on the current joint angles, enabling the end-effector to achieve the adjusted Cartesian pose. The main innovation of this paper lies in augmenting traditional offline optimal planning with real-time adjustment capabilities, achieving a fusion of offline planning and online planning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge