Machine-Learning Interatomic Potentials for Long-Range Systems

Machine-learning interatomic potentials have emerged as a revolutionary class of force-field models in molecular simulations, delivering quantum-mechanical accuracy at a fraction of the computational cost and enabling the simulation of large-scale systems over extended timescales. However, they often focus on modeling local environments, neglecting crucial long-range interactions. We propose a Sum-of-Gaussians Neural Network (SOG-Net), a lightweight and versatile framework for integrating long-range interactions into machine learning force field. The SOG-Net employs a latent-variable learning network that seamlessly bridges short-range and long-range components, coupled with an efficient Fourier convolution layer that incorporates long-range effects. By learning sum-of-Gaussian multipliers across different convolution layers, the SOG-Net adaptively captures diverse long-range decay behaviors while maintaining close-to-linear computational complexity during training and simulation via non-uniform fast Fourier transforms. The method is demonstrated effective for a broad range of long-range systems.

TGPT-PINN: Nonlinear model reduction with transformed GPT-PINNs

We introduce the Transformed Generative Pre-Trained Physics-Informed Neural Networks (TGPT-PINN) for accomplishing nonlinear model order reduction (MOR) of transport-dominated partial differential equations in an MOR-integrating PINNs framework. Building on the recent development of the GPT-PINN that is a network-of-networks design achieving snapshot-based model reduction, we design and test a novel paradigm for nonlinear model reduction that can effectively tackle problems with parameter-dependent discontinuities. Through incorporation of a shock-capturing loss function component as well as a parameter-dependent transform layer, the TGPT-PINN overcomes the limitations of linear model reduction in the transport-dominated regime. We demonstrate this new capability for nonlinear model reduction in the PINNs framework by several nontrivial parametric partial differential equations.

A random-batch Monte Carlo method for many-body systems with singular kernels

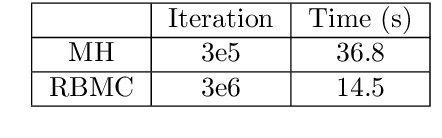
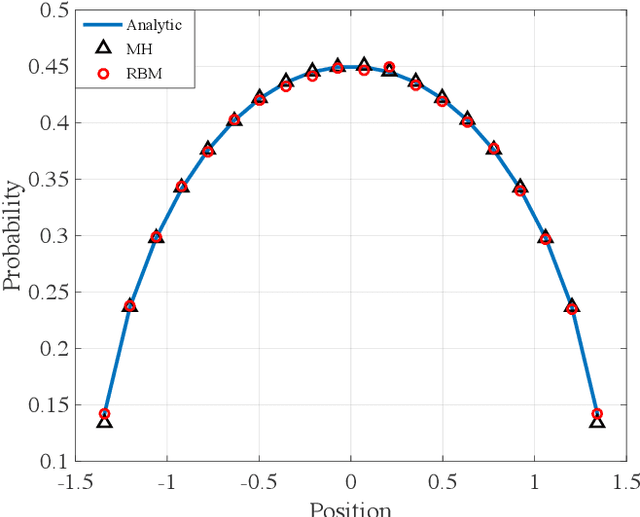
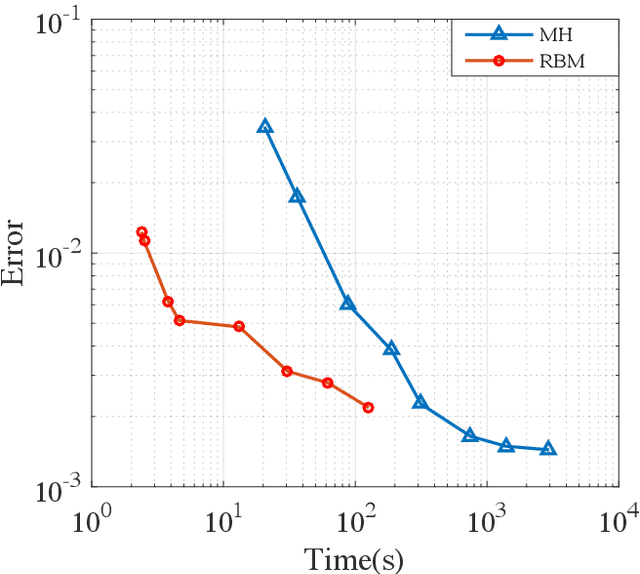
We propose a fast potential splitting Markov Chain Monte Carlo method which costs $O(1)$ time each step for sampling from equilibrium distributions (Gibbs measures) corresponding to particle systems with singular interacting kernels. We decompose the interacting potential into two parts, one is of long range but is smooth, and the other one is of short range but may be singular. To displace a particle, we first evolve a selected particle using the stochastic differential equation (SDE) under the smooth part with the idea of random batches, as commonly used in stochastic gradient Langevin dynamics. Then, we use the short range part to do a Metropolis rejection. Different from the classical Langevin dynamics, we only run the SDE dynamics with random batch for a short duration of time so that the cost in the first step is $O(p)$, where $p$ is the batch size. The cost of the rejection step is $O(1)$ since the interaction used is of short range. We justify the proposed random-batch Monte Carlo method, which combines the random batch and splitting strategies, both in theory and with numerical experiments. While giving comparable results for typical examples of the Dyson Brownian motion and Lennard-Jones fluids, our method can save more time when compared to the classical Metropolis-Hastings algorithm.