Semiparametric Bayesian Difference-in-Differences

This paper studies semiparametric Bayesian inference for the average treatment effect on the treated (ATT) within the difference-in-differences research design. We propose two new Bayesian methods with frequentist validity. The first one places a standard Gaussian process prior on the conditional mean function of the control group. We obtain asymptotic equivalence of our Bayesian estimator and an efficient frequentist estimator by establishing a semiparametric Bernstein-von Mises (BvM) theorem. The second method is a double robust Bayesian procedure that adjusts the prior distribution of the conditional mean function and subsequently corrects the posterior distribution of the resulting ATT. We establish a semiparametric BvM result under double robust smoothness conditions; i.e., the lack of smoothness of conditional mean functions can be compensated by high regularity of the propensity score, and vice versa. Monte Carlo simulations and an empirical application demonstrate that the proposed Bayesian DiD methods exhibit strong finite-sample performance compared to existing frequentist methods. Finally, we outline an extension to difference-in-differences with multiple periods and staggered entry.

Double Robust Bayesian Inference on Average Treatment Effects

We study a double robust Bayesian inference procedure on the average treatment effect (ATE) under unconfoundedness. Our Bayesian approach involves a correction term for prior distributions adjusted by the propensity score. We prove asymptotic equivalence of our Bayesian estimator and efficient frequentist estimators by establishing a new semiparametric Bernstein-von Mises theorem under double robustness; i.e., the lack of smoothness of conditional mean functions can be compensated by high regularity of the propensity score and vice versa. Consequently, the resulting Bayesian point estimator internalizes the bias correction as the frequentist-type doubly robust estimator, and the Bayesian credible sets form confidence intervals with asymptotically exact coverage probability. In simulations, we find that this corrected Bayesian procedure leads to significant bias reduction of point estimation and accurate coverage of confidence intervals, especially when the dimensionality of covariates is large relative to the sample size and the underlying functions become complex. We illustrate our method in an application to the National Supported Work Demonstration.

Rethinking Feature Uncertainty in Stochastic Neural Networks for Adversarial Robustness

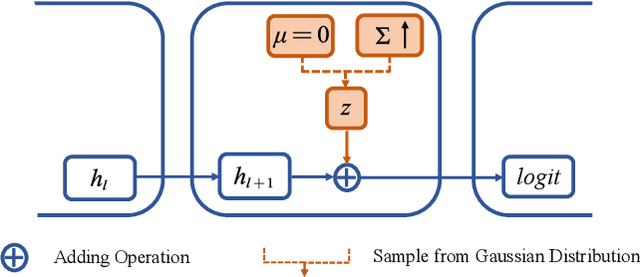
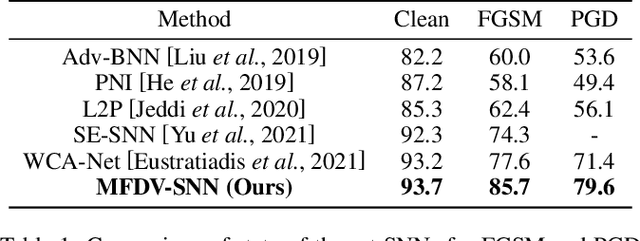
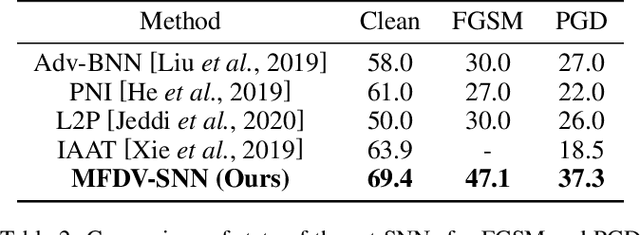
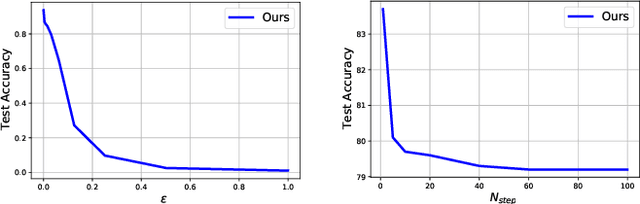
It is well-known that deep neural networks (DNNs) have shown remarkable success in many fields. However, when adding an imperceptible magnitude perturbation on the model input, the model performance might get rapid decrease. To address this issue, a randomness technique has been proposed recently, named Stochastic Neural Networks (SNNs). Specifically, SNNs inject randomness into the model to defend against unseen attacks and improve the adversarial robustness. However, existed studies on SNNs mainly focus on injecting fixed or learnable noises to model weights/activations. In this paper, we find that the existed SNNs performances are largely bottlenecked by the feature representation ability. Surprisingly, simply maximizing the variance per dimension of the feature distribution leads to a considerable boost beyond all previous methods, which we named maximize feature distribution variance stochastic neural network (MFDV-SNN). Extensive experiments on well-known white- and black-box attacks show that MFDV-SNN achieves a significant improvement over existing methods, which indicates that it is a simple but effective method to improve model robustness.