Reducing Discretization Error in the Frank-Wolfe Method

The Frank-Wolfe algorithm is a popular method in structurally constrained machine learning applications, due to its fast per-iteration complexity. However, one major limitation of the method is a slow rate of convergence that is difficult to accelerate due to erratic, zig-zagging step directions, even asymptotically close to the solution. We view this as an artifact of discretization; that is to say, the Frank-Wolfe \emph{flow}, which is its trajectory at asymptotically small step sizes, does not zig-zag, and reducing discretization error will go hand-in-hand in producing a more stabilized method, with better convergence properties. We propose two improvements: a multistep Frank-Wolfe method that directly applies optimized higher-order discretization schemes; and an LMO-averaging scheme with reduced discretization error, and whose local convergence rate over general convex sets accelerates from a rate of $O(1/k)$ to up to $O(1/k^{3/2})$.

A Multistep Frank-Wolfe Method

The Frank-Wolfe algorithm has regained much interest in its use in structurally constrained machine learning applications. However, one major limitation of the Frank-Wolfe algorithm is the slow local convergence property due to the zig-zagging behavior. We observe the zig-zagging phenomenon in the Frank-Wolfe method as an artifact of discretization, and propose multistep Frank-Wolfe variants where the truncation errors decay as $O(\Delta^p)$, where $p$ is the method's order. This strategy "stabilizes" the method, and allows tools like line search and momentum to have more benefits. However, our results suggest that the worst case convergence rate of Runge-Kutta-type discretization schemes cannot improve upon that of the vanilla Frank-Wolfe method for a rate depending on $k$. Still, we believe that this analysis adds to the growing knowledge of flow analysis for optimization methods, and is a cautionary tale on the ultimate usefulness of multistep methods.

Accelerating Frank-Wolfe via Averaging Step Directions

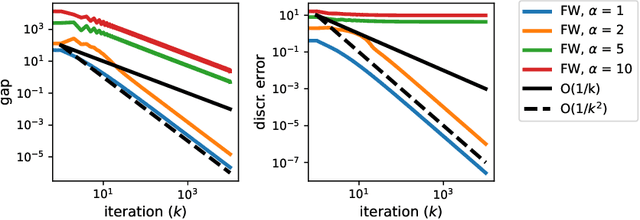
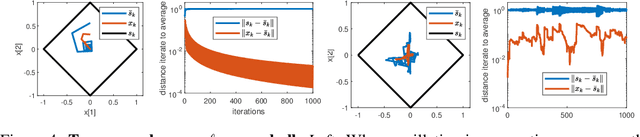
The Frank-Wolfe method is a popular method in sparse constrained optimization, due to its fast per-iteration complexity. However, the tradeoff is that its worst case global convergence is comparatively slow, and importantly, is fundamentally slower than its flow rate--that is to say, the convergence rate is throttled by discretization error. In this work, we consider a modified Frank-Wolfe where the step direction is a simple weighted average of past oracle calls. This method requires very little memory and computational overhead, and provably decays this discretization error term. Numerically, we show that this method improves the convergence rate over several problems, especially after the sparse manifold has been detected. Theoretically, we show the method has an overall global convergence rate of $O(1/k^p)$, where $0< p < 1$; after manifold identification, this rate speeds to $O(1/k^{3p/2})$. We also observe that the method achieves this accelerated rate from a very early stage, suggesting a promising mode of acceleration for this family of methods.

Efficient Construction of Nonlinear Models overNormalized Data

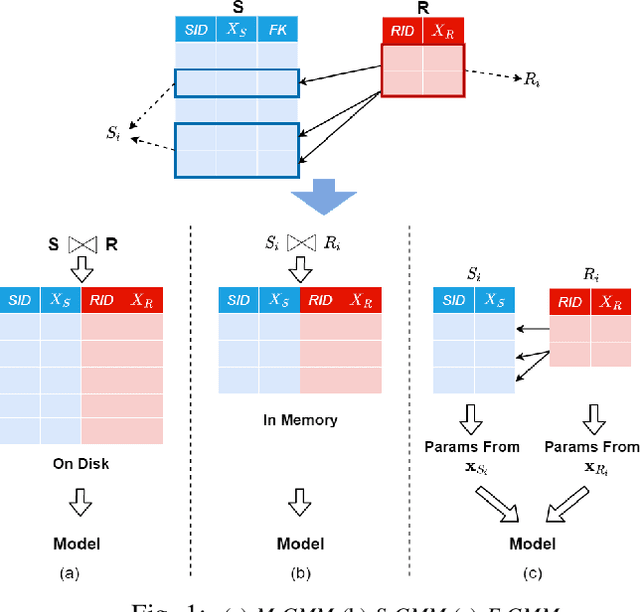
Machine Learning (ML) applications are proliferating in the enterprise. Relational data which are prevalent in enterprise applications are typically normalized; as a result, data has to be denormalized via primary/foreign-key joins to be provided as input to ML algorithms. In this paper, we study the implementation of popular nonlinear ML models, Gaussian Mixture Models (GMM) and Neural Networks (NN), over normalized data addressing both cases of binary and multi-way joins over normalized relations. For the case of GMM, we show how it is possible to decompose computation in a systematic way both for binary joins and for multi-way joins to construct mixture models. We demonstrate that by factoring the computation, one can conduct the training of the models much faster compared to other applicable approaches, without any loss in accuracy. For the case of NN, we propose algorithms to train the network taking normalized data as the input. Similarly, we present algorithms that can conduct the training of the network in a factorized way and offer performance advantages. The redundancy introduced by denormalization can be exploited for certain types of activation functions. However, we demonstrate that attempting to explore this redundancy is helpful up to a certain point; exploring redundancy at higher layers of the network will always result in increased costs and is not recommended. We present the results of a thorough experimental evaluation, varying several parameters of the input relations involved and demonstrate that our proposals for the training of GMM and NN yield drastic performance improvements typically starting at 100%, which become increasingly higher as parameters of the underlying data vary, without any loss in accuracy.