A Bi-level Nonlinear Eigenvector Algorithm for Wasserstein Discriminant Analysis

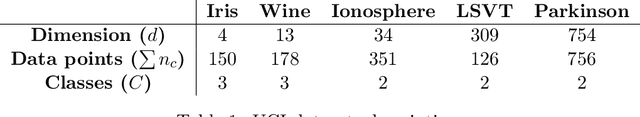
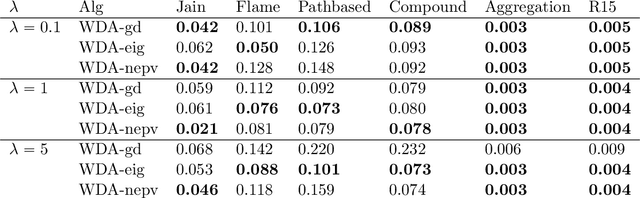
Much like the classical Fisher linear discriminant analysis, Wasserstein discriminant analysis (WDA) is a supervised linear dimensionality reduction method that seeks a projection matrix to maximize the dispersion of different data classes and minimize the dispersion of same data classes. However, in contrast, WDA can account for both global and local inter-connections between data classes using a regularized Wasserstein distance. WDA is formulated as a bi-level nonlinear trace ratio optimization. In this paper, we present a bi-level nonlinear eigenvector (NEPv) algorithm, called WDA-nepv. The inner kernel of WDA-nepv for computing the optimal transport matrix of the regularized Wasserstein distance is formulated as an NEPv, and meanwhile the outer kernel for the trace ratio optimization is also formulated as another NEPv. Consequently, both kernels can be computed efficiently via self-consistent-field iterations and modern solvers for linear eigenvalue problems. Comparing with the existing algorithms for WDA, WDA-nepv is derivative-free and surrogate-model-free. The computational efficiency and applications in classification accuracy of WDA-nepv are demonstrated using synthetic and real-life datasets.

Scalable Spectral Clustering with Group Fairness Constraints

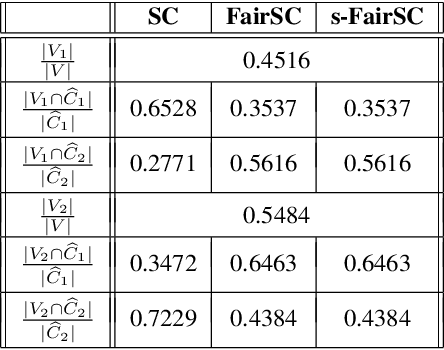
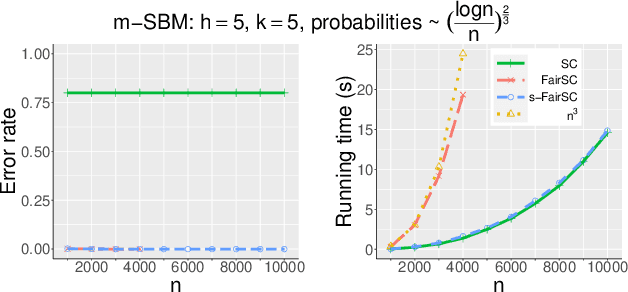
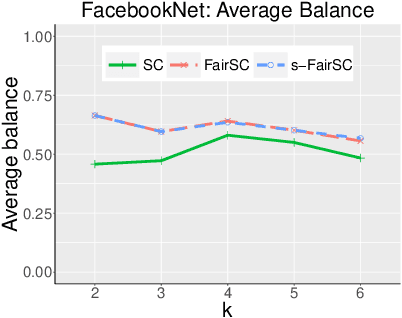
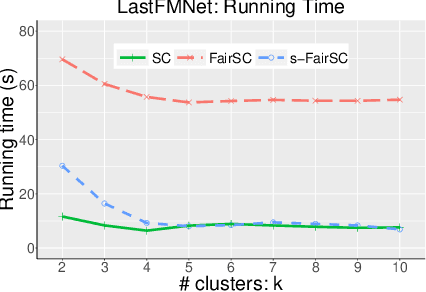
There are synergies of research interests and industrial efforts in modeling fairness and correcting algorithmic bias in machine learning. In this paper, we present a scalable algorithm for spectral clustering (SC) with group fairness constraints. Group fairness is also known as statistical parity where in each cluster, each protected group is represented with the same proportion as in the entirety. While FairSC algorithm (Kleindessner et al., 2019) is able to find the fairer clustering, it is compromised by high costs due to the kernels of computing nullspaces and the square roots of dense matrices explicitly. We present a new formulation of underlying spectral computation by incorporating nullspace projection and Hotelling's deflation such that the resulting algorithm, called s-FairSC, only involves the sparse matrix-vector products and is able to fully exploit the sparsity of the fair SC model. The experimental results on the modified stochastic block model demonstrate that s-FairSC is comparable with FairSC in recovering fair clustering. Meanwhile, it is sped up by a factor of 12 for moderate model sizes. s-FairSC is further demonstrated to be scalable in the sense that the computational costs of s-FairSC only increase marginally compared to the SC without fairness constraints.

Linear Constrained Rayleigh Quotient Optimization: Theory and Algorithms

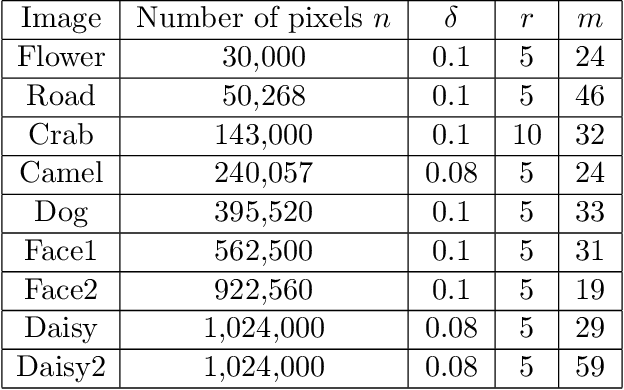
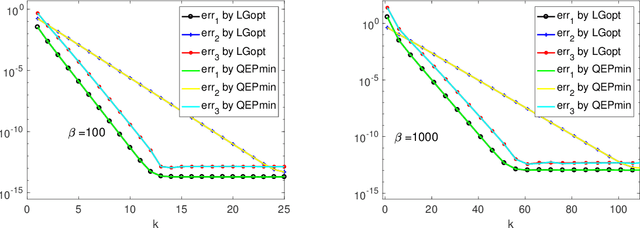
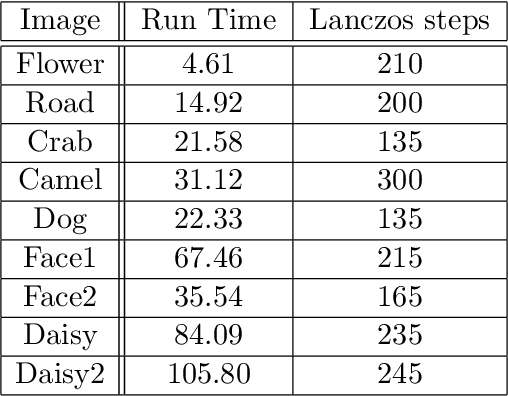
We consider the following constrained Rayleigh quotient optimization problem (CRQopt) $$ \min_{x\in \mathbb{R}^n} x^{T}Ax\,\,\mbox{subject to}\,\, x^{T}x=1\,\mbox{and}\,C^{T}x=b, $$ where $A$ is an $n\times n$ real symmetric matrix and $C$ is an $n\times m$ real matrix. Usually, $m\ll n$. The problem is also known as the constrained eigenvalue problem in the literature because it becomes an eigenvalue problem if the linear constraint $C^{T}x=b$ is removed. We start by equivalently transforming CRQopt into an optimization problem, called LGopt, of minimizing the Lagrangian multiplier of CRQopt, and then an problem, called QEPmin, of finding the smallest eigenvalue of a quadratic eigenvalue problem. Although such equivalences has been discussed in the literature, it appears to be the first time that these equivalences are rigorously justified. Then we propose to numerically solve LGopt and QEPmin by the Krylov subspace projection method via the Lanczos process. The basic idea, as the Lanczos method for the symmetric eigenvalue problem, is to first reduce LGopt and QEPmin by projecting them onto Krylov subspaces to yield problems of the same types but of much smaller sizes, and then solve the reduced problems by some direct methods, which is either a secular equation solver (in the case of LGopt) or an eigensolver (in the case of QEPmin). The resulting algorithm is called the Lanczos algorithm. We perform convergence analysis for the proposed method and obtain error bounds. The sharpness of the error bound is demonstrated by artificial examples, although in applications the method often converges much faster than the bounds suggest. Finally, we apply the Lanczos algorithm to semi-supervised learning in the context of constrained clustering.

A Self-consistent-field Iteration for Orthogonal Canonical Correlation Analysis

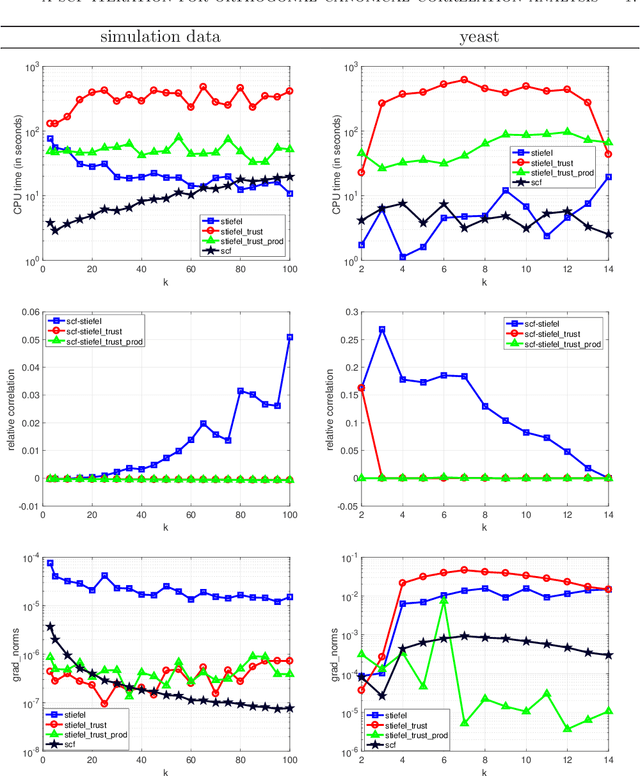
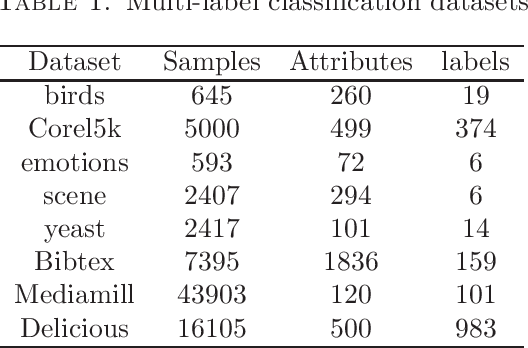
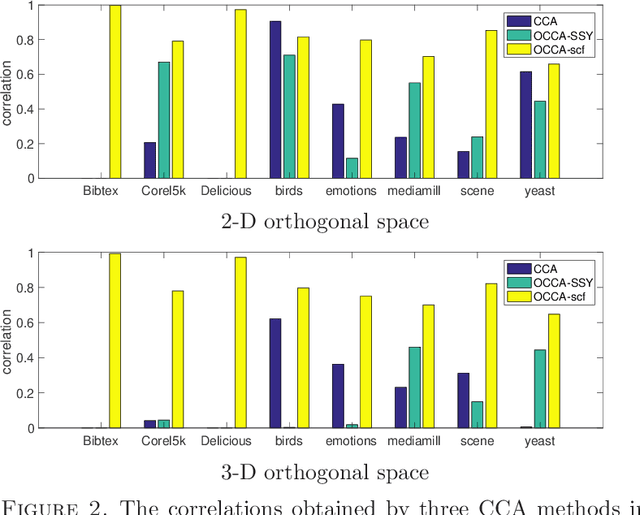
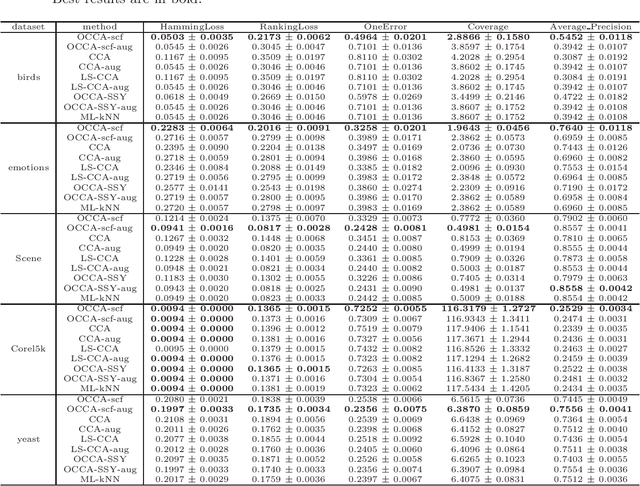
We propose an efficient algorithm for solving orthogonal canonical correlation analysis (OCCA) in the form of trace-fractional structure and orthogonal linear projections. Even though orthogonality has been widely used and proved to be a useful criterion for pattern recognition and feature extraction, existing methods for solving OCCA problem are either numerical unstable by relying on a deflation scheme, or less efficient by directly using generic optimization methods. In this paper, we propose an alternating numerical scheme whose core is the sub-maximization problem in the trace-fractional form with an orthogonal constraint. A customized self-consistent-field (SCF) iteration for this sub-maximization problem is devised. It is proved that the SCF iteration is globally convergent to a KKT point and that the alternating numerical scheme always converges. We further formulate a new trace-fractional maximization problem for orthogonal multiset CCA (OMCCA) and then propose an efficient algorithm with an either Jacobi-style or Gauss-Seidel-style updating scheme based on the same SCF iteration. Extensive experiments are conducted to evaluate the proposed algorithms against existing methods including two real world applications: multi-label classification and multi-view feature extraction. Experimental results show that our methods not only perform competitively to or better than baselines but also are more efficient.