Leihong Zhang
Orthogonal Multi-view Analysis by Successive Approximations via Eigenvectors
Oct 04, 2020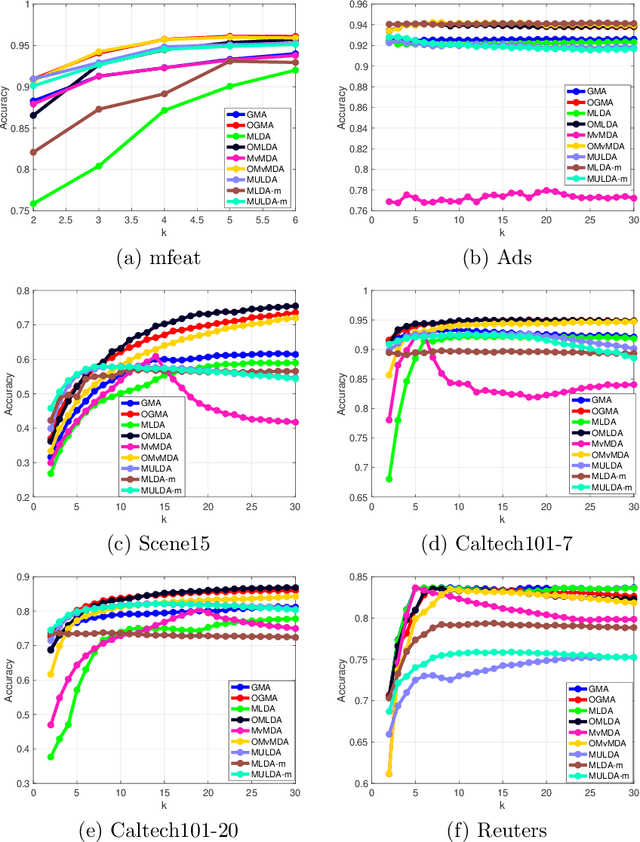
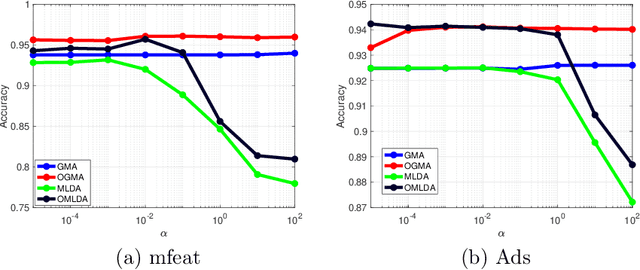
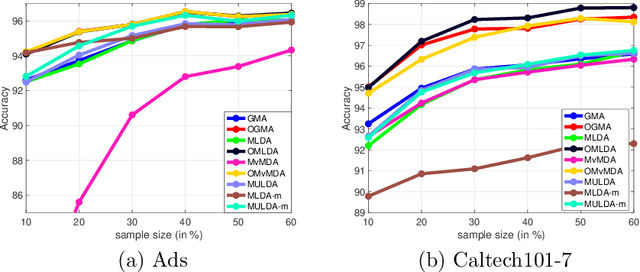
Abstract:We propose a unified framework for multi-view subspace learning to learn individual orthogonal projections for all views. The framework integrates the correlations within multiple views, supervised discriminant capacity, and distance preservation in a concise and compact way. It not only includes several existing models as special cases, but also inspires new novel models. To demonstrate its versatility to handle different learning scenarios, we showcase three new multi-view discriminant analysis models and two new multi-view multi-label classification ones under this framework. An efficient numerical method based on successive approximations via eigenvectors is presented to solve the associated optimization problem. The method is built upon an iterative Krylov subspace method which can easily scale up for high-dimensional datasets. Extensive experiments are conducted on various real-world datasets for multi-view discriminant analysis and multi-view multi-label classification. The experimental results demonstrate that the proposed models are consistently competitive to and often better than the compared methods that do not learn orthogonal projections.
A Self-consistent-field Iteration for Orthogonal Canonical Correlation Analysis
Sep 25, 2019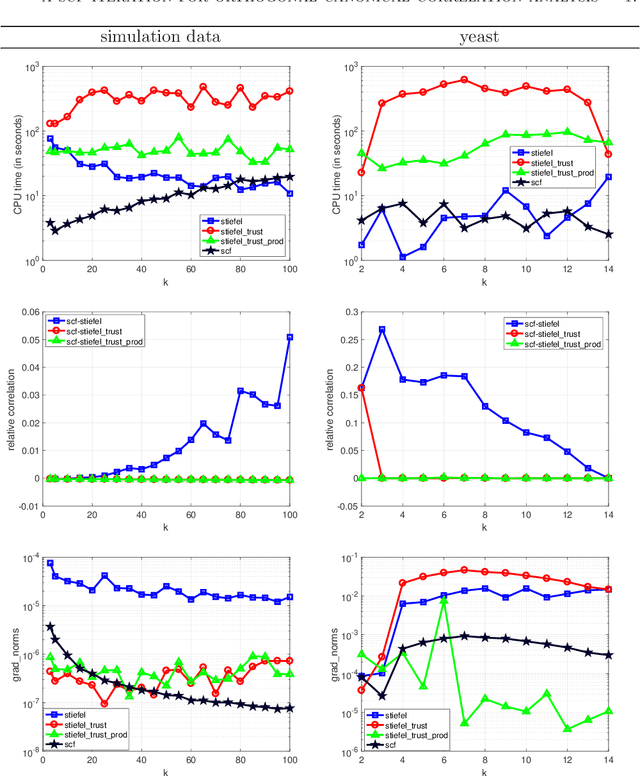
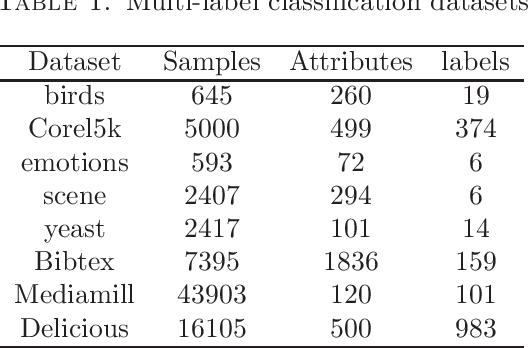
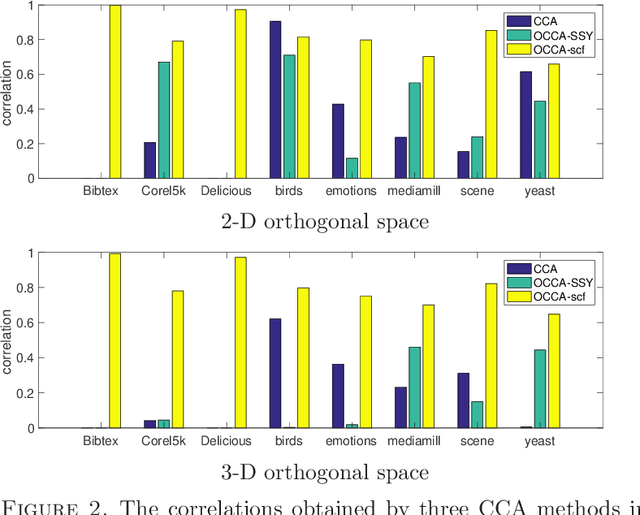
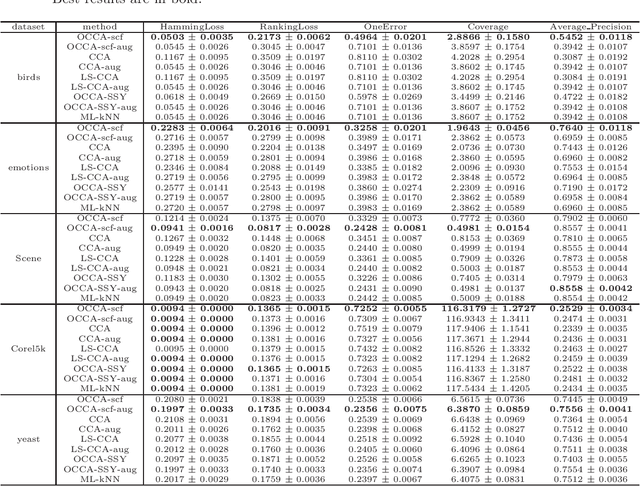
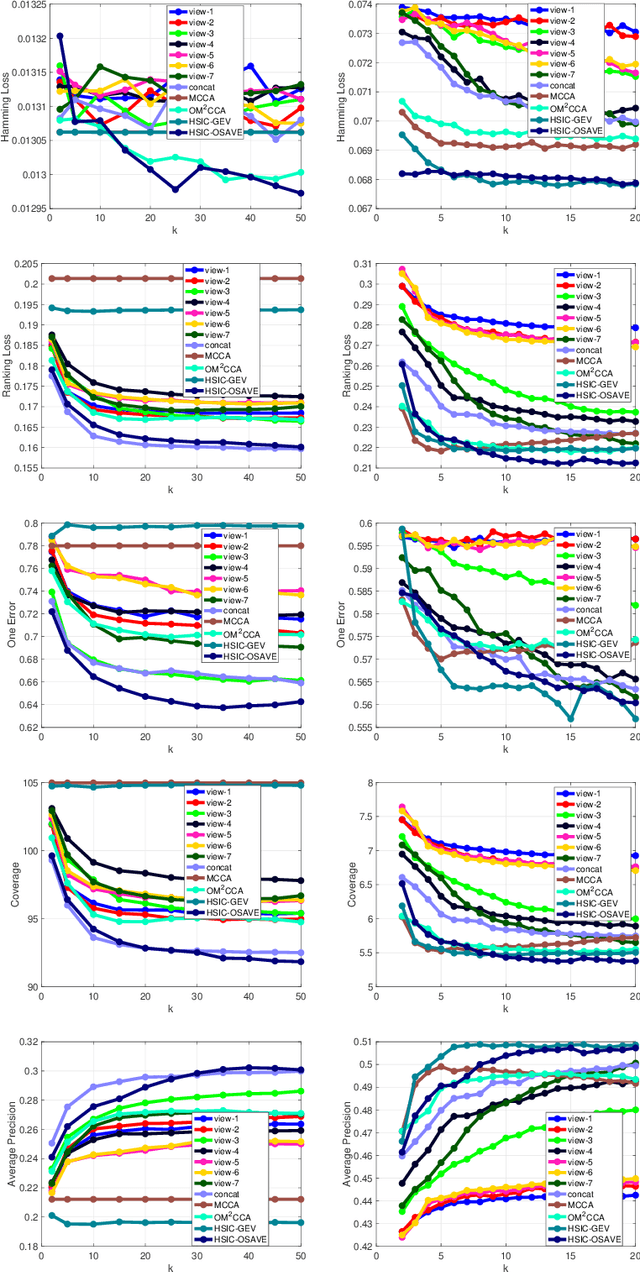
Abstract:We propose an efficient algorithm for solving orthogonal canonical correlation analysis (OCCA) in the form of trace-fractional structure and orthogonal linear projections. Even though orthogonality has been widely used and proved to be a useful criterion for pattern recognition and feature extraction, existing methods for solving OCCA problem are either numerical unstable by relying on a deflation scheme, or less efficient by directly using generic optimization methods. In this paper, we propose an alternating numerical scheme whose core is the sub-maximization problem in the trace-fractional form with an orthogonal constraint. A customized self-consistent-field (SCF) iteration for this sub-maximization problem is devised. It is proved that the SCF iteration is globally convergent to a KKT point and that the alternating numerical scheme always converges. We further formulate a new trace-fractional maximization problem for orthogonal multiset CCA (OMCCA) and then propose an efficient algorithm with an either Jacobi-style or Gauss-Seidel-style updating scheme based on the same SCF iteration. Extensive experiments are conducted to evaluate the proposed algorithms against existing methods including two real world applications: multi-label classification and multi-view feature extraction. Experimental results show that our methods not only perform competitively to or better than baselines but also are more efficient.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge