Orthogonal Multi-view Analysis by Successive Approximations via Eigenvectors
Paper and Code
Oct 04, 2020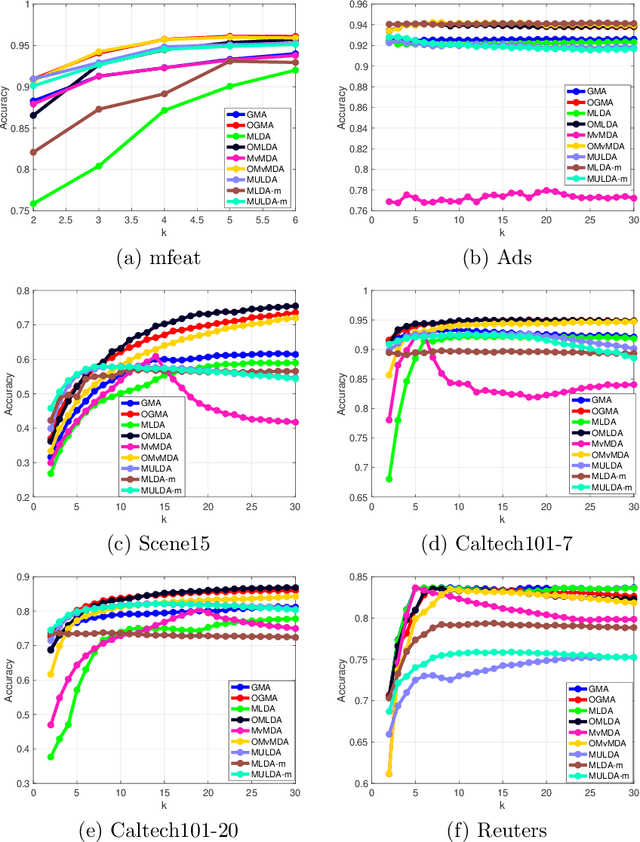
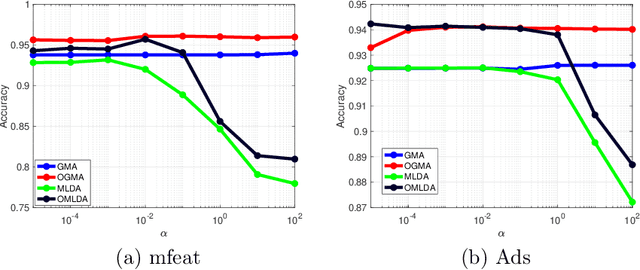
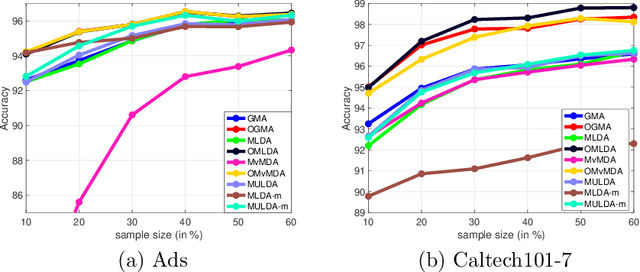
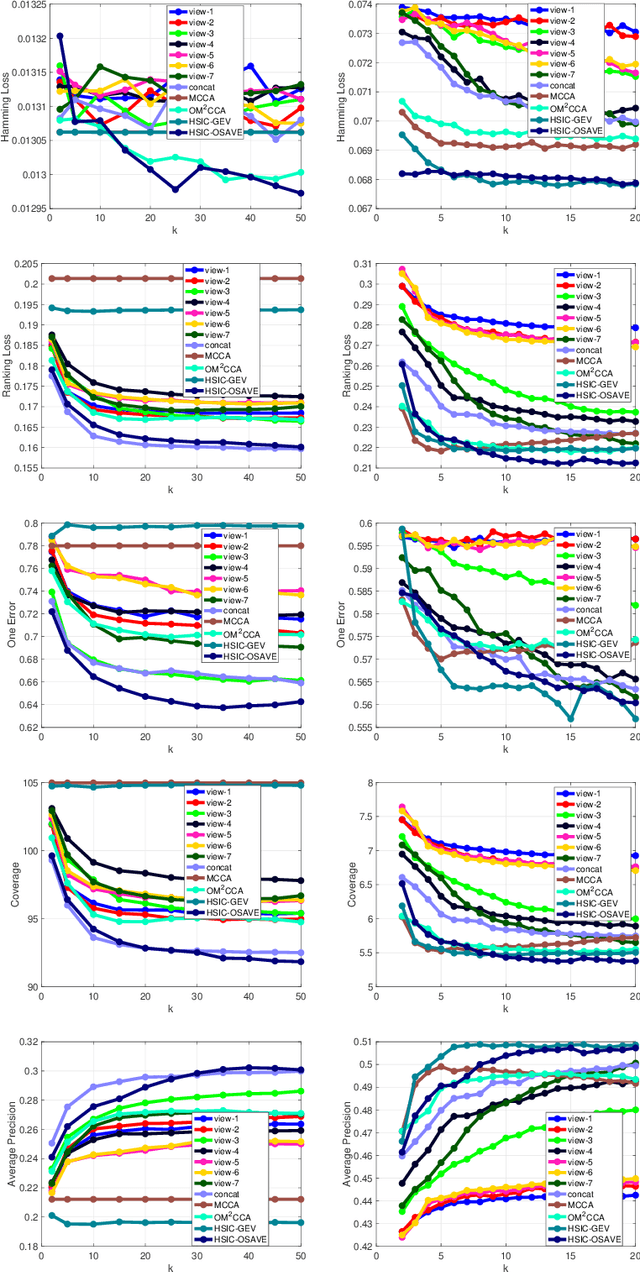
We propose a unified framework for multi-view subspace learning to learn individual orthogonal projections for all views. The framework integrates the correlations within multiple views, supervised discriminant capacity, and distance preservation in a concise and compact way. It not only includes several existing models as special cases, but also inspires new novel models. To demonstrate its versatility to handle different learning scenarios, we showcase three new multi-view discriminant analysis models and two new multi-view multi-label classification ones under this framework. An efficient numerical method based on successive approximations via eigenvectors is presented to solve the associated optimization problem. The method is built upon an iterative Krylov subspace method which can easily scale up for high-dimensional datasets. Extensive experiments are conducted on various real-world datasets for multi-view discriminant analysis and multi-view multi-label classification. The experimental results demonstrate that the proposed models are consistently competitive to and often better than the compared methods that do not learn orthogonal projections.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge