Chungen Shen
Uncorrelated Semi-paired Subspace Learning
Nov 22, 2020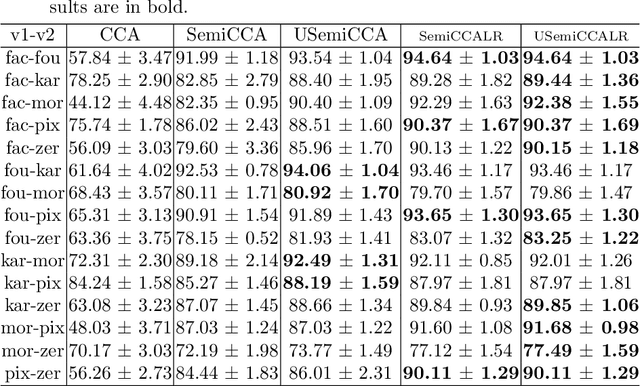

Abstract:Multi-view datasets are increasingly collected in many real-world applications, and we have seen better learning performance by existing multi-view learning methods than by conventional single-view learning methods applied to each view individually. But, most of these multi-view learning methods are built on the assumption that at each instance no view is missing and all data points from all views must be perfectly paired. Hence they cannot handle unpaired data but ignore them completely from their learning process. However, unpaired data can be more abundant in reality than paired ones and simply ignoring all unpaired data incur tremendous waste in resources. In this paper, we focus on learning uncorrelated features by semi-paired subspace learning, motivated by many existing works that show great successes of learning uncorrelated features. Specifically, we propose a generalized uncorrelated multi-view subspace learning framework, which can naturally integrate many proven learning criteria on the semi-paired data. To showcase the flexibility of the framework, we instantiate five new semi-paired models for both unsupervised and semi-supervised learning. We also design a successive alternating approximation (SAA) method to solve the resulting optimization problem and the method can be combined with the powerful Krylov subspace projection technique if needed. Extensive experimental results on multi-view feature extraction and multi-modality classification show that our proposed models perform competitively to or better than the baselines.
Orthogonal Multi-view Analysis by Successive Approximations via Eigenvectors
Oct 04, 2020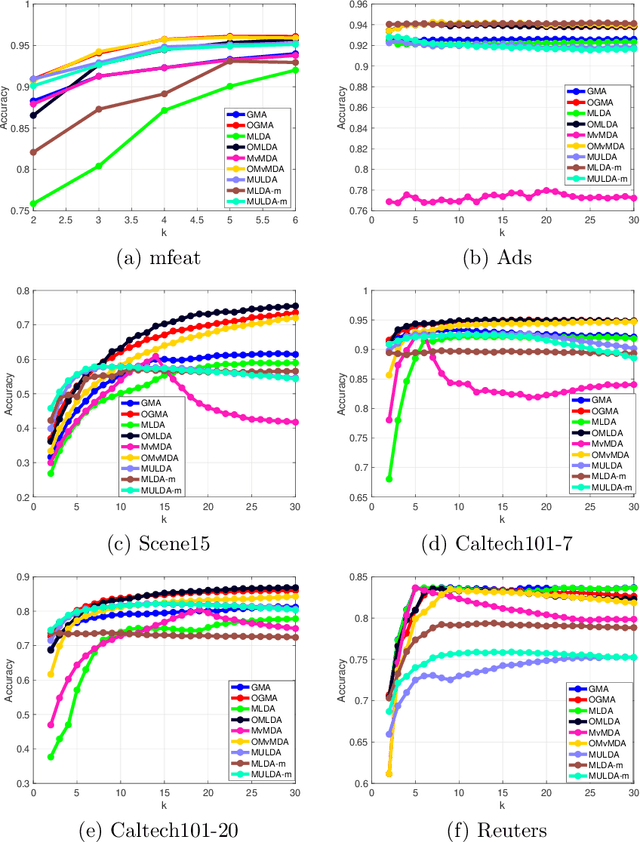
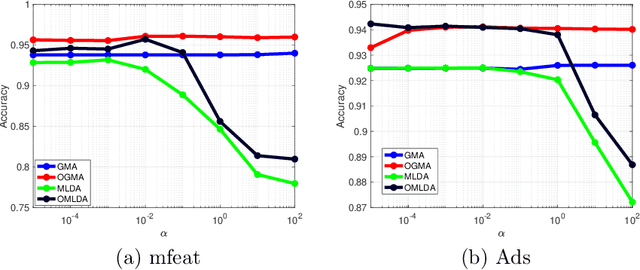
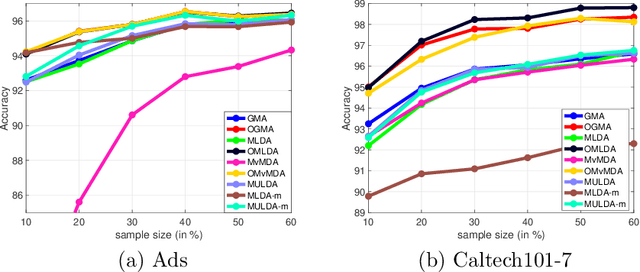
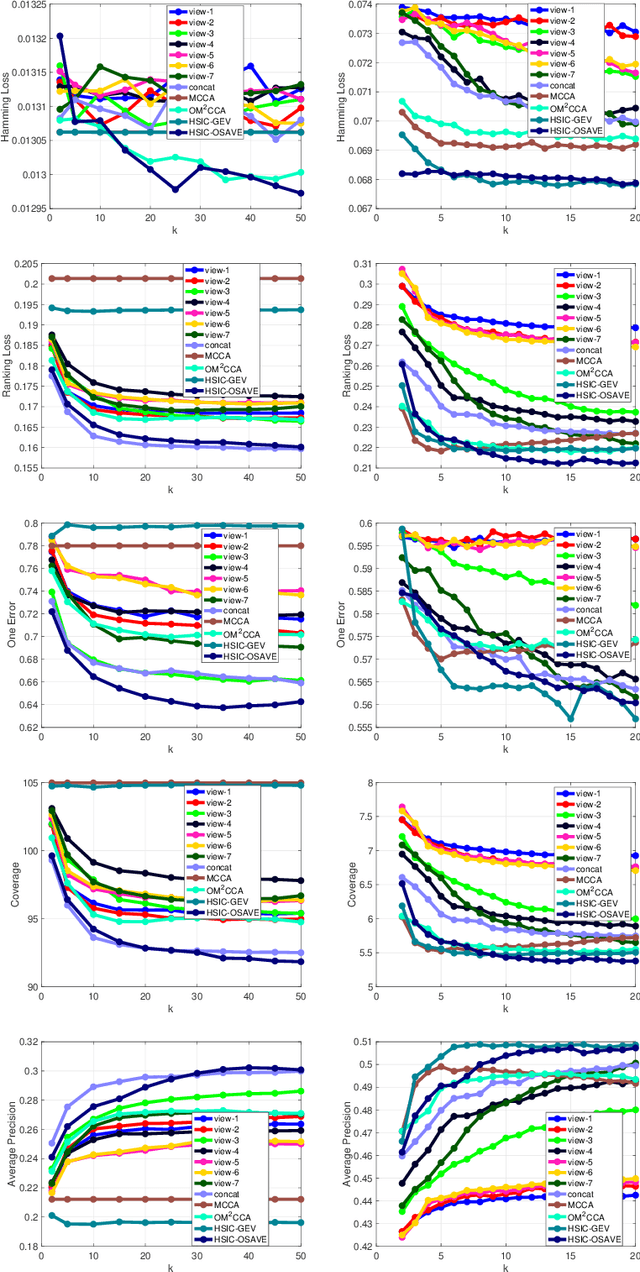
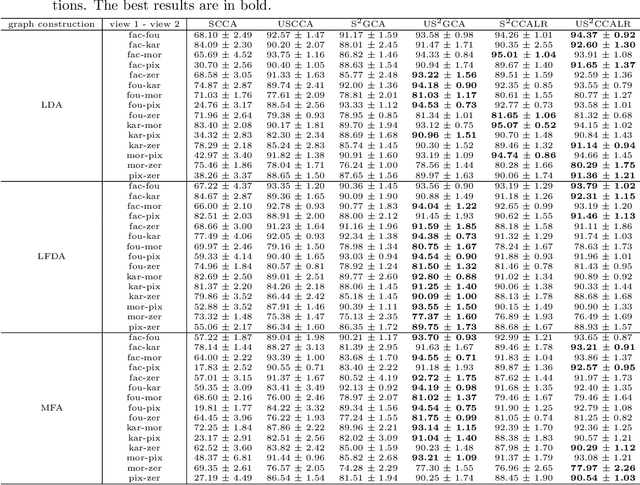
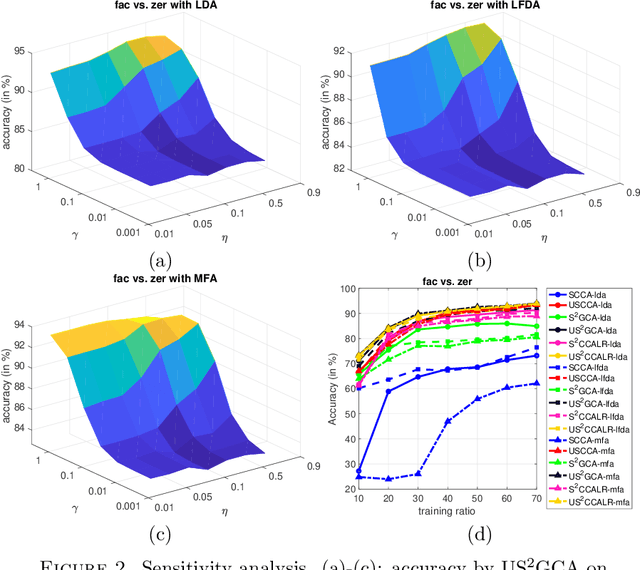
Abstract:We propose a unified framework for multi-view subspace learning to learn individual orthogonal projections for all views. The framework integrates the correlations within multiple views, supervised discriminant capacity, and distance preservation in a concise and compact way. It not only includes several existing models as special cases, but also inspires new novel models. To demonstrate its versatility to handle different learning scenarios, we showcase three new multi-view discriminant analysis models and two new multi-view multi-label classification ones under this framework. An efficient numerical method based on successive approximations via eigenvectors is presented to solve the associated optimization problem. The method is built upon an iterative Krylov subspace method which can easily scale up for high-dimensional datasets. Extensive experiments are conducted on various real-world datasets for multi-view discriminant analysis and multi-view multi-label classification. The experimental results demonstrate that the proposed models are consistently competitive to and often better than the compared methods that do not learn orthogonal projections.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge