Ren-Cang Li
Trace Ratio Optimization with an Application to Multi-view Learning
Jan 12, 2021


Abstract:A trace ratio optimization problem over the Stiefel manifold is investigated from the perspectives of both theory and numerical computations. At least three special cases of the problem have arisen from Fisher linear discriminant analysis, canonical correlation analysis, and unbalanced Procrustes problem, respectively. Necessary conditions in the form of nonlinear eigenvalue problem with eigenvector dependency are established and a numerical method based on the self-consistent field (SCF) iteration is designed and proved to be always convergent. As an application to multi-view subspace learning, a new framework and its instantiated concrete models are proposed and demonstrated on real world data sets. Numerical results show that the efficiency of the proposed numerical methods and effectiveness of the new multi-view subspace learning models.
Uncorrelated Semi-paired Subspace Learning
Nov 22, 2020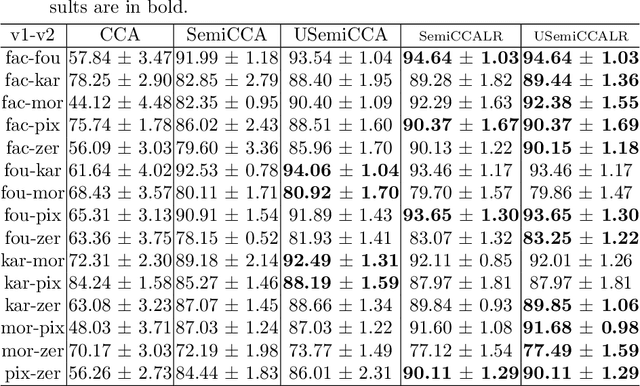

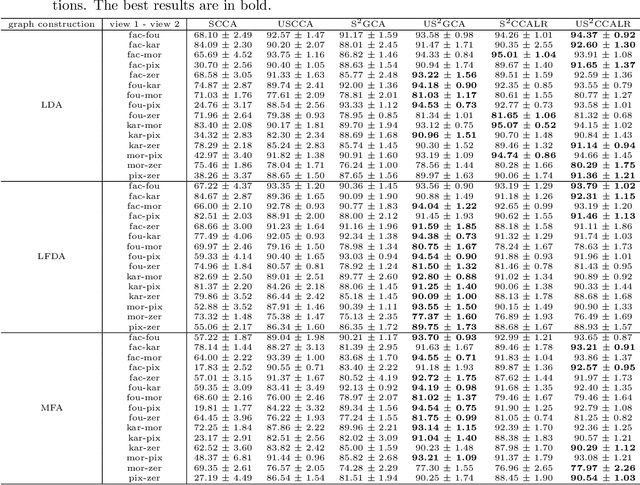
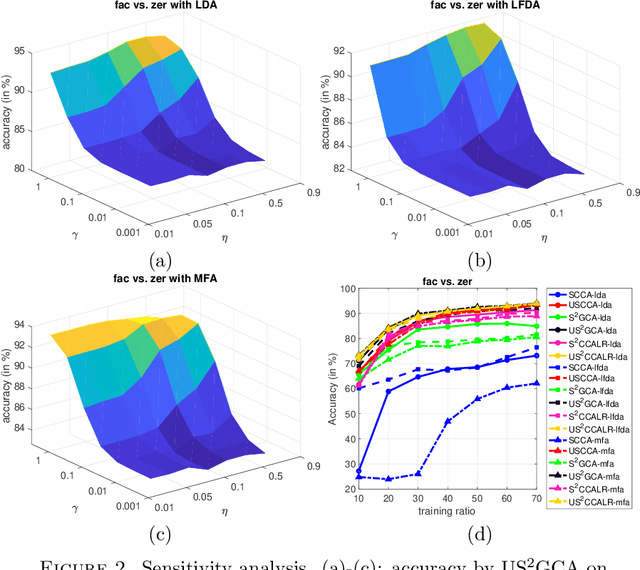
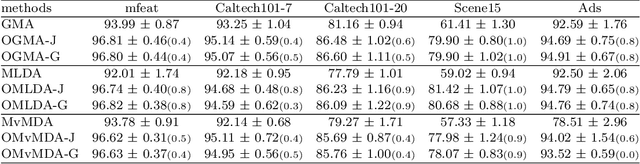
Abstract:Multi-view datasets are increasingly collected in many real-world applications, and we have seen better learning performance by existing multi-view learning methods than by conventional single-view learning methods applied to each view individually. But, most of these multi-view learning methods are built on the assumption that at each instance no view is missing and all data points from all views must be perfectly paired. Hence they cannot handle unpaired data but ignore them completely from their learning process. However, unpaired data can be more abundant in reality than paired ones and simply ignoring all unpaired data incur tremendous waste in resources. In this paper, we focus on learning uncorrelated features by semi-paired subspace learning, motivated by many existing works that show great successes of learning uncorrelated features. Specifically, we propose a generalized uncorrelated multi-view subspace learning framework, which can naturally integrate many proven learning criteria on the semi-paired data. To showcase the flexibility of the framework, we instantiate five new semi-paired models for both unsupervised and semi-supervised learning. We also design a successive alternating approximation (SAA) method to solve the resulting optimization problem and the method can be combined with the powerful Krylov subspace projection technique if needed. Extensive experimental results on multi-view feature extraction and multi-modality classification show that our proposed models perform competitively to or better than the baselines.
Multi-view Orthonormalized Partial Least Squares: Regularizations and Deep Extensions
Jul 09, 2020


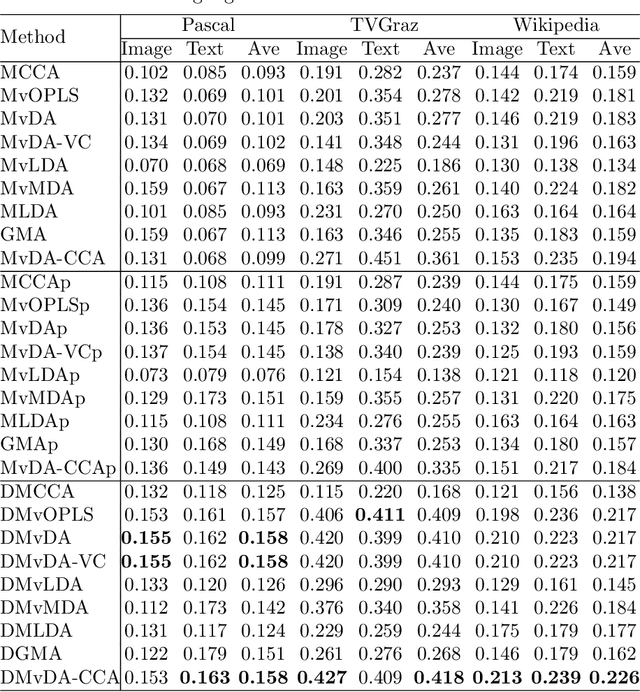
Abstract:We establish a family of subspace-based learning method for multi-view learning using the least squares as the fundamental basis. Specifically, we investigate orthonormalized partial least squares (OPLS) and study its important properties for both multivariate regression and classification. Building on the least squares reformulation of OPLS, we propose a unified multi-view learning framework to learn a classifier over a common latent space shared by all views. The regularization technique is further leveraged to unleash the power of the proposed framework by providing three generic types of regularizers on its inherent ingredients including model parameters, decision values and latent projected points. We instantiate a set of regularizers in terms of various priors. The proposed framework with proper choices of regularizers not only can recast existing methods, but also inspire new models. To further improve the performance of the proposed framework on complex real problems, we propose to learn nonlinear transformations parameterized by deep networks. Extensive experiments are conducted to compare various methods on nine data sets with different numbers of views in terms of both feature extraction and cross-modal retrieval.
Linear Constrained Rayleigh Quotient Optimization: Theory and Algorithms
Nov 07, 2019
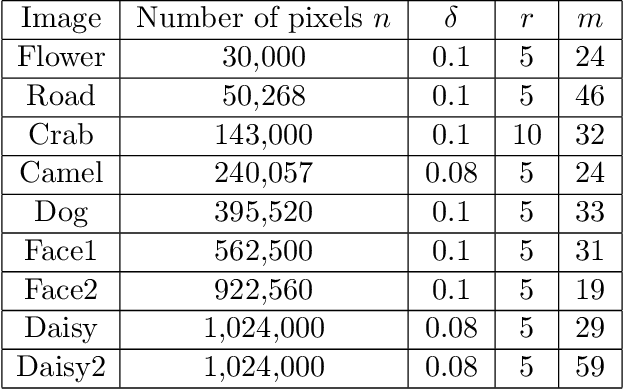
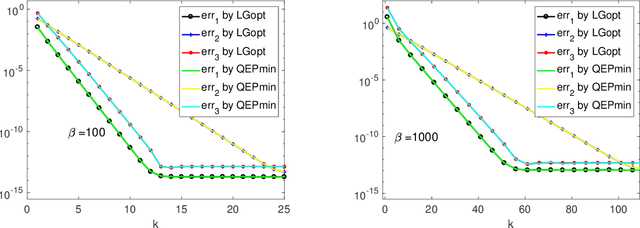
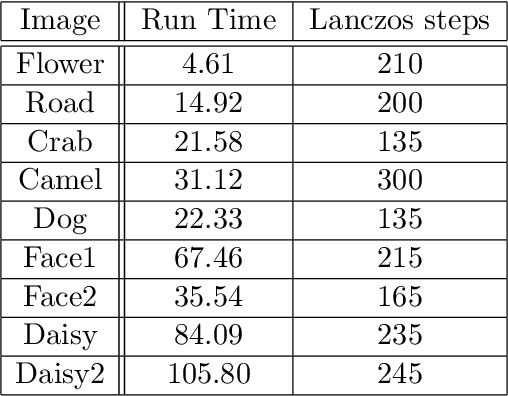
Abstract:We consider the following constrained Rayleigh quotient optimization problem (CRQopt) $$ \min_{x\in \mathbb{R}^n} x^{T}Ax\,\,\mbox{subject to}\,\, x^{T}x=1\,\mbox{and}\,C^{T}x=b, $$ where $A$ is an $n\times n$ real symmetric matrix and $C$ is an $n\times m$ real matrix. Usually, $m\ll n$. The problem is also known as the constrained eigenvalue problem in the literature because it becomes an eigenvalue problem if the linear constraint $C^{T}x=b$ is removed. We start by equivalently transforming CRQopt into an optimization problem, called LGopt, of minimizing the Lagrangian multiplier of CRQopt, and then an problem, called QEPmin, of finding the smallest eigenvalue of a quadratic eigenvalue problem. Although such equivalences has been discussed in the literature, it appears to be the first time that these equivalences are rigorously justified. Then we propose to numerically solve LGopt and QEPmin by the Krylov subspace projection method via the Lanczos process. The basic idea, as the Lanczos method for the symmetric eigenvalue problem, is to first reduce LGopt and QEPmin by projecting them onto Krylov subspaces to yield problems of the same types but of much smaller sizes, and then solve the reduced problems by some direct methods, which is either a secular equation solver (in the case of LGopt) or an eigensolver (in the case of QEPmin). The resulting algorithm is called the Lanczos algorithm. We perform convergence analysis for the proposed method and obtain error bounds. The sharpness of the error bound is demonstrated by artificial examples, although in applications the method often converges much faster than the bounds suggest. Finally, we apply the Lanczos algorithm to semi-supervised learning in the context of constrained clustering.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge