Multi-view Orthonormalized Partial Least Squares: Regularizations and Deep Extensions
Paper and Code
Jul 09, 2020


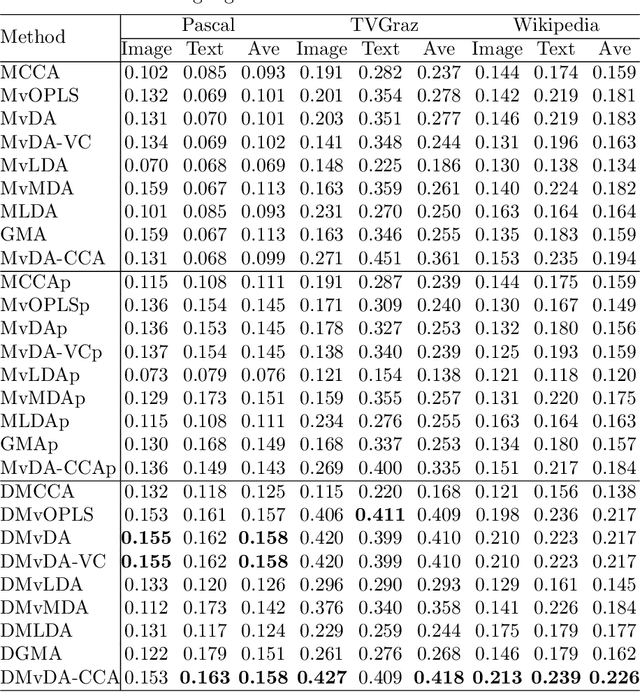
We establish a family of subspace-based learning method for multi-view learning using the least squares as the fundamental basis. Specifically, we investigate orthonormalized partial least squares (OPLS) and study its important properties for both multivariate regression and classification. Building on the least squares reformulation of OPLS, we propose a unified multi-view learning framework to learn a classifier over a common latent space shared by all views. The regularization technique is further leveraged to unleash the power of the proposed framework by providing three generic types of regularizers on its inherent ingredients including model parameters, decision values and latent projected points. We instantiate a set of regularizers in terms of various priors. The proposed framework with proper choices of regularizers not only can recast existing methods, but also inspire new models. To further improve the performance of the proposed framework on complex real problems, we propose to learn nonlinear transformations parameterized by deep networks. Extensive experiments are conducted to compare various methods on nine data sets with different numbers of views in terms of both feature extraction and cross-modal retrieval.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge