Zhantao Deng
Reconstruction of Manipulated Garment with Guided Deformation Prior
May 17, 2024Abstract:Modeling the shape of garments has received much attention, but most existing approaches assume the garments to be worn by someone, which constrains the range of shapes they can assume. In this work, we address shape recovery when garments are being manipulated instead of worn, which gives rise to an even larger range of possible shapes. To this end, we leverage the implicit sewing patterns (ISP) model for garment modeling and extend it by adding a diffusion-based deformation prior to represent these shapes. To recover 3D garment shapes from incomplete 3D point clouds acquired when the garment is folded, we map the points to UV space, in which our priors are learned, to produce partial UV maps, and then fit the priors to recover complete UV maps and 2D to 3D mappings. Experimental results demonstrate the superior reconstruction accuracy of our method compared to previous ones, especially when dealing with large non-rigid deformations arising from the manipulations.
Better Patch Stitching for Parametric Surface Reconstruction
Oct 14, 2020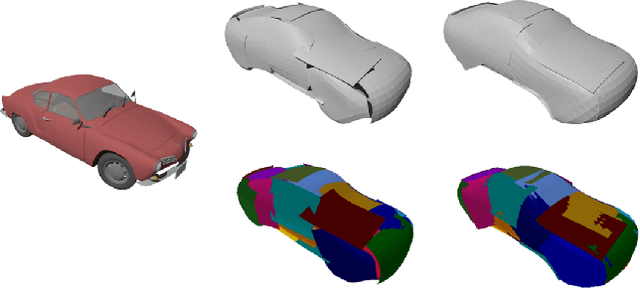
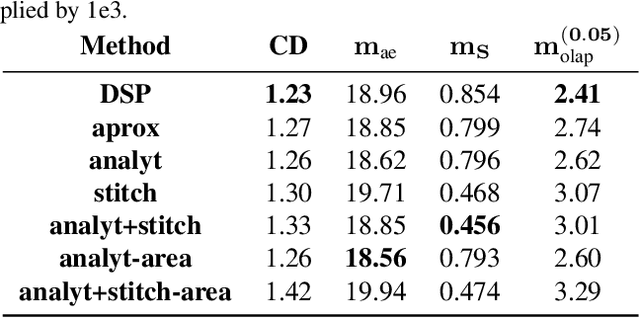
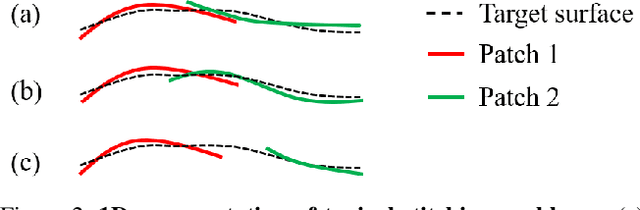
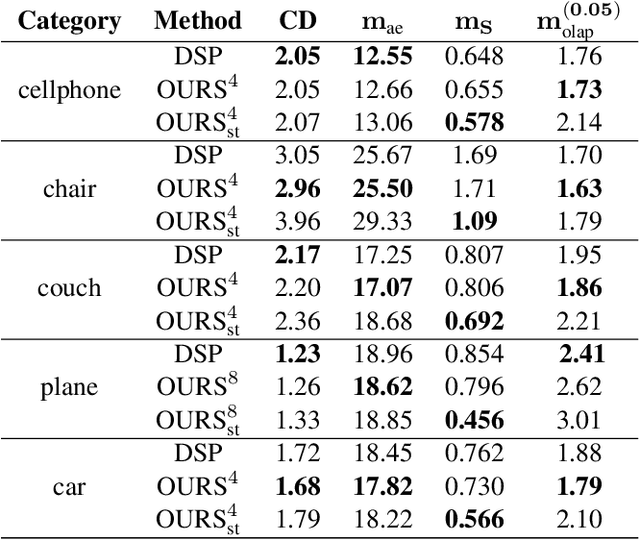
Abstract:Recently, parametric mappings have emerged as highly effective surface representations, yielding low reconstruction error. In particular, the latest works represent the target shape as an atlas of multiple mappings, which can closely encode object parts. Atlas representations, however, suffer from one major drawback: The individual mappings are not guaranteed to be consistent, which results in holes in the reconstructed shape or in jagged surface areas. We introduce an approach that explicitly encourages global consistency of the local mappings. To this end, we introduce two novel loss terms. The first term exploits the surface normals and requires that they remain locally consistent when estimated within and across the individual mappings. The second term further encourages better spatial configuration of the mappings by minimizing novel stitching error. We show on standard benchmarks that the use of normal consistency requirement outperforms the baselines quantitatively while enforcing better stitching leads to much better visual quality of the reconstructed objects as compared to the state-of-the-art.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge