Better Patch Stitching for Parametric Surface Reconstruction
Paper and Code
Oct 14, 2020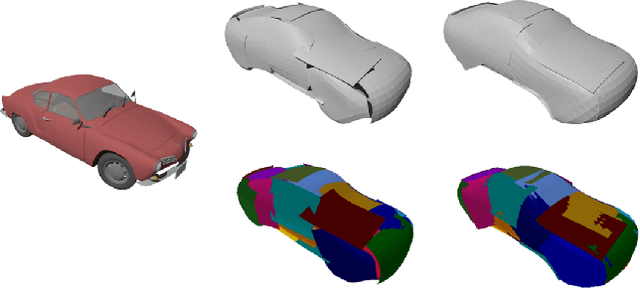
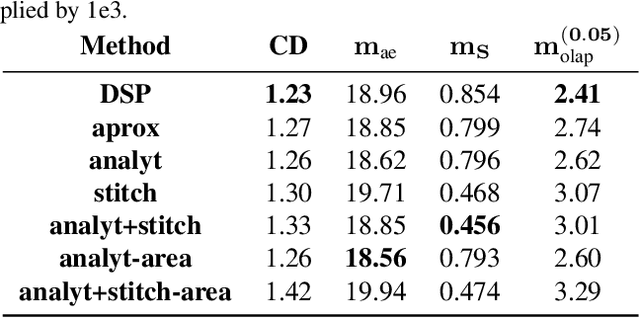
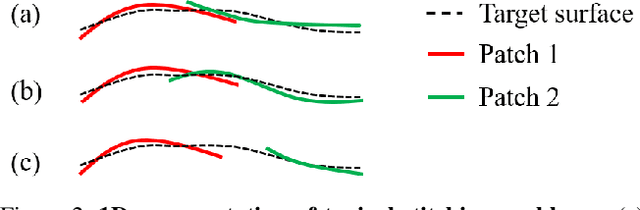
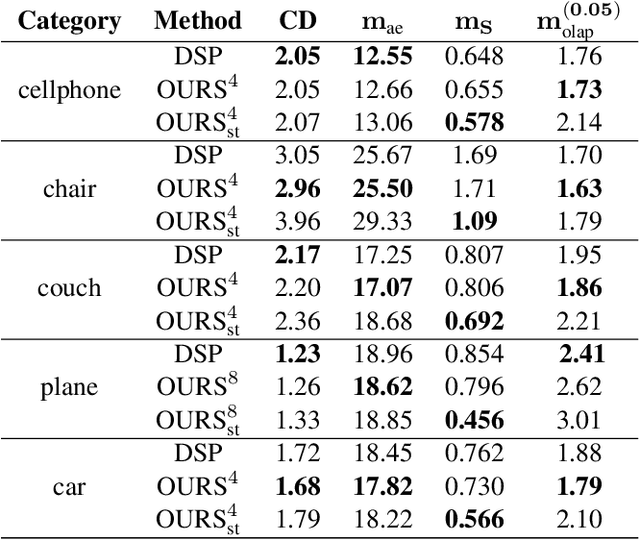
Recently, parametric mappings have emerged as highly effective surface representations, yielding low reconstruction error. In particular, the latest works represent the target shape as an atlas of multiple mappings, which can closely encode object parts. Atlas representations, however, suffer from one major drawback: The individual mappings are not guaranteed to be consistent, which results in holes in the reconstructed shape or in jagged surface areas. We introduce an approach that explicitly encourages global consistency of the local mappings. To this end, we introduce two novel loss terms. The first term exploits the surface normals and requires that they remain locally consistent when estimated within and across the individual mappings. The second term further encourages better spatial configuration of the mappings by minimizing novel stitching error. We show on standard benchmarks that the use of normal consistency requirement outperforms the baselines quantitatively while enforcing better stitching leads to much better visual quality of the reconstructed objects as compared to the state-of-the-art.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge