Physics of Language Models: Part 3.1, Knowledge Storage and Extraction

Large language models can store extensive world knowledge, often extractable through question-answering (e.g., "What is Abraham Lincoln's birthday?"). However, it's unclear whether the model answers questions based on exposure to exact/similar questions during training, or if it genuinely extracts knowledge from the source (e.g., Wikipedia biographies). In this paper, we conduct an in-depth study of this problem using a controlled set of semi-synthetic biography data. We uncover a relationship between the model's knowledge extraction ability and different diversity measures of the training data. We conduct (nearly) linear probing, revealing a strong correlation between this relationship and whether the model (nearly) linearly encodes the knowledge attributes at the hidden embedding of the entity names, or across the embeddings of other tokens in the training text.

Local Graph Clustering Beyond Cheeger's Inequality

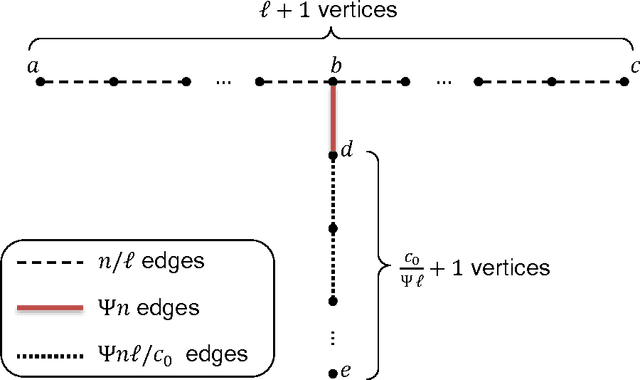
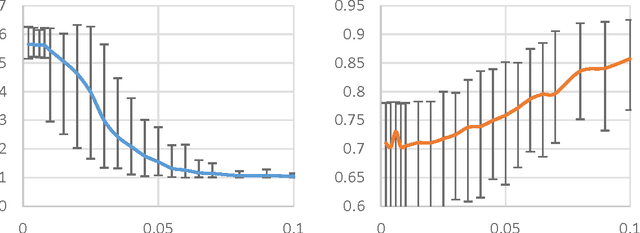
Motivated by applications of large-scale graph clustering, we study random-walk-based LOCAL algorithms whose running times depend only on the size of the output cluster, rather than the entire graph. All previously known such algorithms guarantee an output conductance of $\tilde{O}(\sqrt{\phi(A)})$ when the target set $A$ has conductance $\phi(A)\in[0,1]$. In this paper, we improve it to $$\tilde{O}\bigg( \min\Big\{\sqrt{\phi(A)}, \frac{\phi(A)}{\sqrt{\mathsf{Conn}(A)}} \Big\} \bigg)\enspace, $$ where the internal connectivity parameter $\mathsf{Conn}(A) \in [0,1]$ is defined as the reciprocal of the mixing time of the random walk over the induced subgraph on $A$. For instance, using $\mathsf{Conn}(A) = \Omega(\lambda(A) / \log n)$ where $\lambda$ is the second eigenvalue of the Laplacian of the induced subgraph on $A$, our conductance guarantee can be as good as $\tilde{O}(\phi(A)/\sqrt{\lambda(A)})$. This builds an interesting connection to the recent advance of the so-called improved Cheeger's Inequality [KKL+13], which says that global spectral algorithms can provide a conductance guarantee of $O(\phi_{\mathsf{opt}}/\sqrt{\lambda_3})$ instead of $O(\sqrt{\phi_{\mathsf{opt}}})$. In addition, we provide theoretical guarantee on the clustering accuracy (in terms of precision and recall) of the output set. We also prove that our analysis is tight, and perform empirical evaluation to support our theory on both synthetic and real data. It is worth noting that, our analysis outperforms prior work when the cluster is well-connected. In fact, the better it is well-connected inside, the more significant improvement (both in terms of conductance and accuracy) we can obtain. Our results shed light on why in practice some random-walk-based algorithms perform better than its previous theory, and help guide future research about local clustering.

Flow-Based Algorithms for Local Graph Clustering

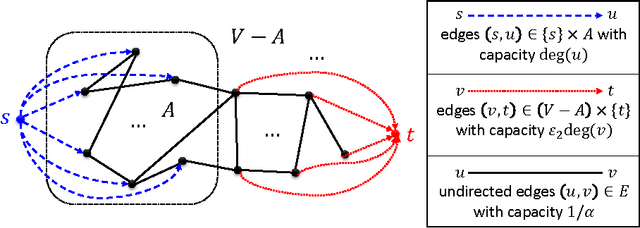
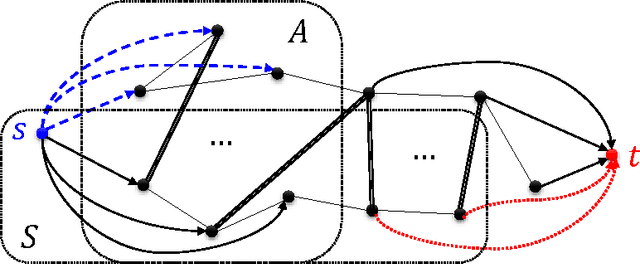
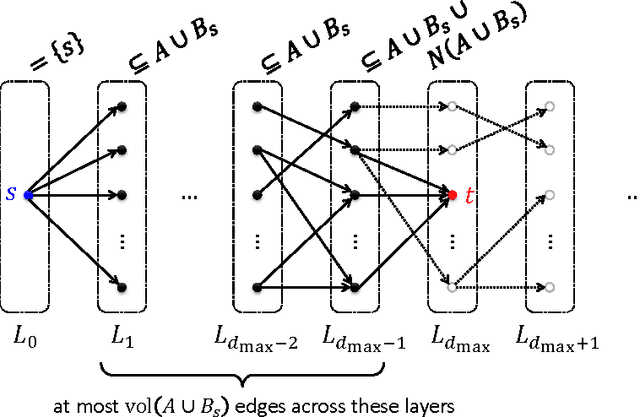
Given a subset S of vertices of an undirected graph G, the cut-improvement problem asks us to find a subset S that is similar to A but has smaller conductance. A very elegant algorithm for this problem has been given by Andersen and Lang [AL08] and requires solving a small number of single-commodity maximum flow computations over the whole graph G. In this paper, we introduce LocalImprove, the first cut-improvement algorithm that is local, i.e. that runs in time dependent on the size of the input set A rather than on the size of the entire graph. Moreover, LocalImprove achieves this local behaviour while essentially matching the same theoretical guarantee as the global algorithm of Andersen and Lang. The main application of LocalImprove is to the design of better local-graph-partitioning algorithms. All previously known local algorithms for graph partitioning are random-walk based and can only guarantee an output conductance of O(\sqrt{OPT}) when the target set has conductance OPT \in [0,1]. Very recently, Zhu, Lattanzi and Mirrokni [ZLM13] improved this to O(OPT / \sqrt{CONN}) where the internal connectivity parameter CONN \in [0,1] is defined as the reciprocal of the mixing time of the random walk over the graph induced by the target set. In this work, we show how to use LocalImprove to obtain a constant approximation O(OPT) as long as CONN/OPT = Omega(1). This yields the first flow-based algorithm. Moreover, its performance strictly outperforms the ones based on random walks and surprisingly matches that of the best known global algorithm, which is SDP-based, in this parameter regime [MMV12]. Finally, our results show that spectral methods are not the only viable approach to the construction of local graph partitioning algorithm and open door to the study of algorithms with even better approximation and locality guarantees.

Survey & Experiment: Towards the Learning Accuracy

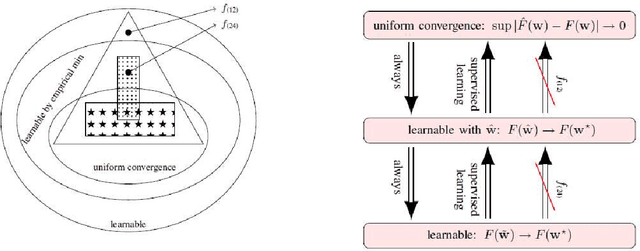
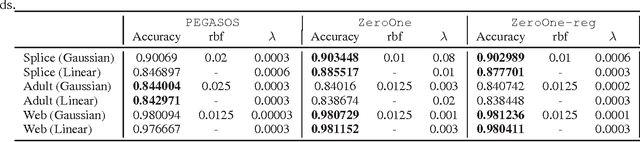
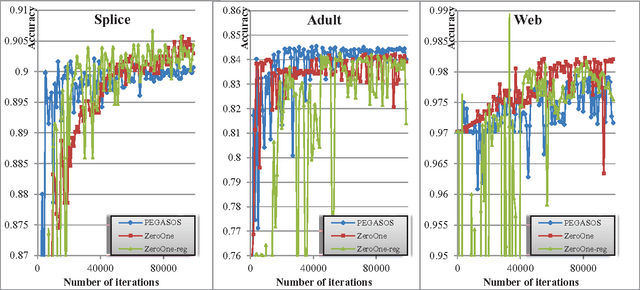
To attain the best learning accuracy, people move on with difficulties and frustrations. Though one can optimize the empirical objective using a given set of samples, its generalization ability to the entire sample distribution remains questionable. Even if a fair generalization guarantee is offered, one still wants to know what is to happen if the regularizer is removed, and/or how well the artificial loss (like the hinge loss) relates to the accuracy. For such reason, this report surveys four different trials towards the learning accuracy, embracing the major advances in supervised learning theory in the past four years. Starting from the generic setting of learning, the first two trials introduce the best optimization and generalization bounds for convex learning, and the third trial gets rid of the regularizer. As an innovative attempt, the fourth trial studies the optimization when the objective is exactly the accuracy, in the special case of binary classification. This report also analyzes the last trial through experiments.