Zeyong Su
A Unified Weight Initialization Paradigm for Tensorial Convolutional Neural Networks
May 28, 2022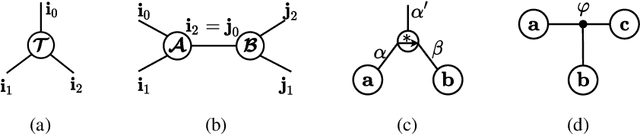
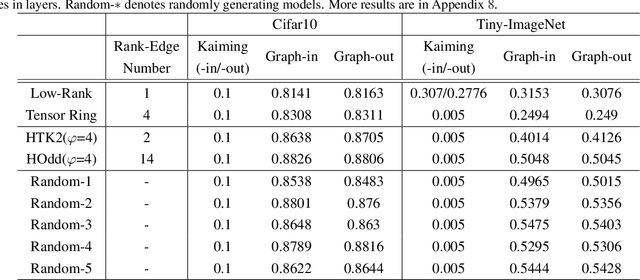
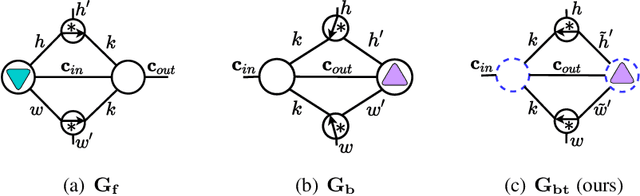

Abstract:Tensorial Convolutional Neural Networks (TCNNs) have attracted much research attention for their power in reducing model parameters or enhancing the generalization ability. However, exploration of TCNNs is hindered even from weight initialization methods. To be specific, general initialization methods, such as Xavier or Kaiming initialization, usually fail to generate appropriate weights for TCNNs. Meanwhile, although there are ad-hoc approaches for specific architectures (e.g., Tensor Ring Nets), they are not applicable to TCNNs with other tensor decomposition methods (e.g., CP or Tucker decomposition). To address this problem, we propose a universal weight initialization paradigm, which generalizes Xavier and Kaiming methods and can be widely applicable to arbitrary TCNNs. Specifically, we first present the Reproducing Transformation to convert the backward process in TCNNs to an equivalent convolution process. Then, based on the convolution operators in the forward and backward processes, we build a unified paradigm to control the variance of features and gradients in TCNNs. Thus, we can derive fan-in and fan-out initialization for various TCNNs. We demonstrate that our paradigm can stabilize the training of TCNNs, leading to faster convergence and better results.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge