Model-based Super-resolution: Towards a Unified Framework for Super-resolution

In mathematics, a super-resolution problem can be formulated as acquiring high-frequency data from low-frequency measurements. This extrapolation problem in the frequency domain is well-known to be unstable. We propose the model-based super-resolution framework (Model-SR) to address this ill-posedness. Within this framework, we can recover the signal by solving a nonlinear least square problem and achieve the super-resolution. Theoretically, the resolution-enhancing map is proved to have Lipschitz continuity under mild conditions, leading to a stable solution to the super-resolution problem. We apply the general theory to three concrete models and give the stability estimates for each model. Numerical experiments are conducted to show the super-resolution behavior of the proposed framework. The model-based mathematical framework can be extended to problems with similar structures.

SCAN-MUSIC: An Efficient Super-resolution Algorithm for Single Snapshot Wide-band Line Spectral Estimation

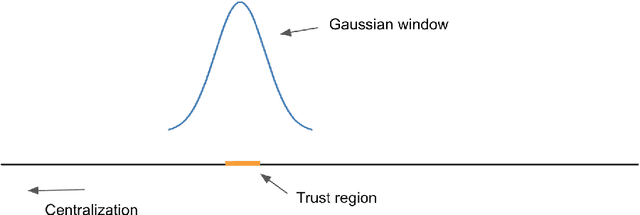
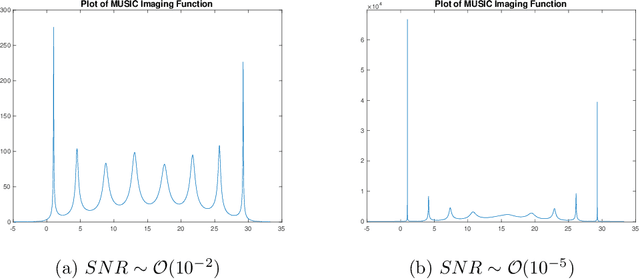
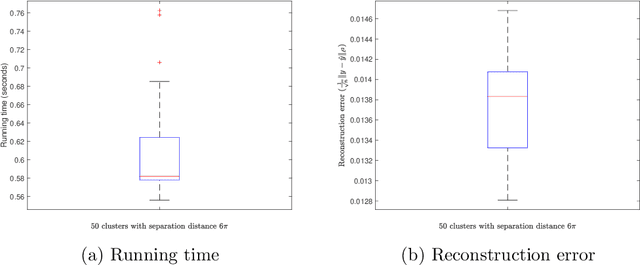
We propose an efficient algorithm for reconstructing one-dimensional wide-band line spectra from their Fourier data in a bounded interval $[-\Omega,\Omega]$. While traditional subspace methods such as MUSIC achieve super-resolution for closely separated line spectra, their computational cost is high, particularly for wide-band line spectra. To address this issue, we proposed a scalable algorithm termed SCAN-MUSIC that scans the spectral domain using a fixed Gaussian window and then reconstructs the line spectra falling into the window at each time. For line spectra with cluster structure, we further refine the proposed algorithm using the annihilating filter technique. Both algorithms can significantly reduce the computational complexity of the standard MUSIC algorithm with a moderate loss of resolution. Moreover, in terms of speed, their performance is comparable to the state-of-the-art algorithms, while being more reliable for reconstructing line spectra with cluster structure. The algorithms are supplemented with theoretical analyses of error estimates, sampling complexity, computational complexity, and computational limit.

PE-YOLO: Pyramid Enhancement Network for Dark Object Detection

Current object detection models have achieved good results on many benchmark datasets, detecting objects in dark conditions remains a large challenge. To address this issue, we propose a pyramid enhanced network (PENet) and joint it with YOLOv3 to build a dark object detection framework named PE-YOLO. Firstly, PENet decomposes the image into four components of different resolutions using the Laplacian pyramid. Specifically we propose a detail processing module (DPM) to enhance the detail of images, which consists of context branch and edge branch. In addition, we propose a low-frequency enhancement filter (LEF) to capture low-frequency semantics and prevent high-frequency noise. PE-YOLO adopts an end-to-end joint training approach and only uses normal detection loss to simplify the training process. We conduct experiments on the low-light object detection dataset ExDark to demonstrate the effectiveness of ours. The results indicate that compared with other dark detectors and low-light enhancement models, PE-YOLO achieves the advanced results, achieving 78.0% in mAP and 53.6 in FPS, respectively, which can adapt to object detection under different low-light conditions. The code is available at https://github.com/XiangchenYin/PE-YOLO.

IFF: A Super-resolution Algorithm for Multiple Measurements

We consider the problem of reconstructing one-dimensional point sources from their Fourier measurements in a bounded interval $[-\Omega, \Omega]$. This problem is known to be challenging in the regime where the spacing of the sources is below the Rayleigh length $\frac{\pi}{\Omega}$. In this paper, we propose a super-resolution algorithm, called Iterative Focusing-localization and Filtering (IFF), to resolve closely spaced point sources from their multiple measurements that are obtained by using multiple unknown illumination patterns. The new proposed algorithm has a distinct feature in that it reconstructs the point sources one by one in an iterative manner and hence requires no prior information about the source numbers. The new feature also allows for a subsampling strategy that can circumvent the computation of singular-value decomposition for large matrices as in the usual subspace methods. A theoretical analysis of the methods behind the algorithm is also provided. The derived results imply a phase transition phenomenon in the reconstruction of source locations which is confirmed in numerical experiments. Numerical results show that the algorithm can achieve a stable reconstruction for point sources with a minimum separation distance that is close to the theoretical limit. The algorithm can be generalized to higher dimensions.