SCAN-MUSIC: An Efficient Super-resolution Algorithm for Single Snapshot Wide-band Line Spectral Estimation
Paper and Code
Oct 27, 2023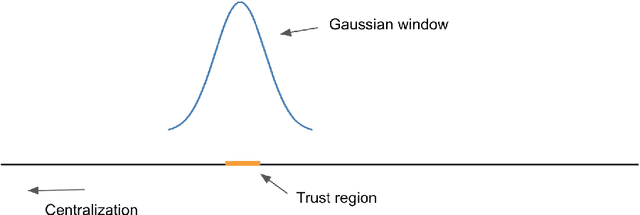

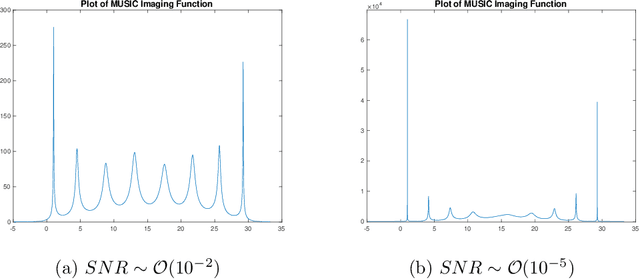
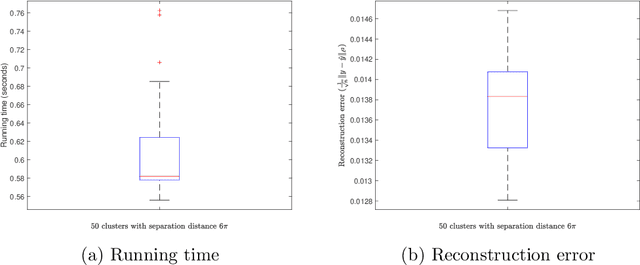
We propose an efficient algorithm for reconstructing one-dimensional wide-band line spectra from their Fourier data in a bounded interval $[-\Omega,\Omega]$. While traditional subspace methods such as MUSIC achieve super-resolution for closely separated line spectra, their computational cost is high, particularly for wide-band line spectra. To address this issue, we proposed a scalable algorithm termed SCAN-MUSIC that scans the spectral domain using a fixed Gaussian window and then reconstructs the line spectra falling into the window at each time. For line spectra with cluster structure, we further refine the proposed algorithm using the annihilating filter technique. Both algorithms can significantly reduce the computational complexity of the standard MUSIC algorithm with a moderate loss of resolution. Moreover, in terms of speed, their performance is comparable to the state-of-the-art algorithms, while being more reliable for reconstructing line spectra with cluster structure. The algorithms are supplemented with theoretical analyses of error estimates, sampling complexity, computational complexity, and computational limit.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge