Fine-Tuning Pre-trained Large Time Series Models for Prediction of Wind Turbine SCADA Data

The remarkable achievements of large models in the fields of natural language processing (NLP) and computer vision (CV) have sparked interest in their application to time series forecasting within industrial contexts. This paper explores the application of a pre-trained large time series model, Timer, which was initially trained on a wide range of time series data from multiple domains, in the prediction of Supervisory Control and Data Acquisition (SCADA) data collected from wind turbines. The model was fine-tuned on SCADA datasets sourced from two wind farms, which exhibited differing characteristics, and its accuracy was subsequently evaluated. Additionally, the impact of data volume was studied to evaluate the few-shot ability of the Timer. Finally, an application study on one-turbine fine-tuning for whole-plant prediction was implemented where both few-shot and cross-turbine generalization capacity is required. The results reveal that the pre-trained large model does not consistently outperform other baseline models in terms of prediction accuracy whenever the data is abundant or not, but demonstrates superior performance in the application study. This result underscores the distinctive advantages of the pre-trained large time series model in facilitating swift deployment.

Domain-specific ReAct for physics-integrated iterative modeling: A case study of LLM agents for gas path analysis of gas turbines

This study explores the application of large language models (LLMs) with callable tools in energy and power engineering domain, focusing on gas path analysis of gas turbines. We developed a dual-agent tool-calling process to integrate expert knowledge, predefined tools, and LLM reasoning. We evaluated various LLMs, including LLama3, Qwen1.5 and GPT. Smaller models struggled with tool usage and parameter extraction, while larger models demonstrated favorable capabilities. All models faced challenges with complex, multi-component problems. Based on the test results, we infer that LLMs with nearly 100 billion parameters could meet professional scenario requirements with fine-tuning and advanced prompt design. Continued development are likely to enhance their accuracy and effectiveness, paving the way for more robust AI-driven solutions.

Solving Inverse Wave Scattering with Deep Learning

This paper proposes a neural network approach for solving two classical problems in the two-dimensional inverse wave scattering: far field pattern problem and seismic imaging. The mathematical problem of inverse wave scattering is to recover the scatterer field of a medium based on the boundary measurement of the scattered wave from the medium, which is high-dimensional and nonlinear. For the far field pattern problem under the circular experimental setup, a perturbative analysis shows that the forward map can be approximated by a vectorized convolution operator in the angular direction. Motivated by this and filtered back-projection, we propose an effective neural network architecture for the inverse map using the recently introduced BCR-Net along with the standard convolution layers. Analogously for the seismic imaging problem, we propose a similar neural network architecture under the rectangular domain setup with a depth-dependent background velocity. Numerical results demonstrate the efficiency of the proposed neural networks.

Solving Traveltime Tomography with Deep Learning

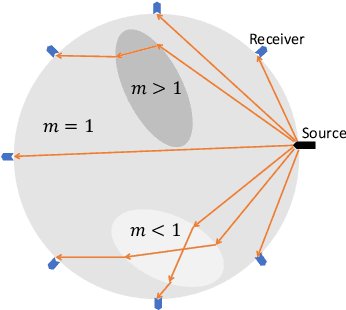
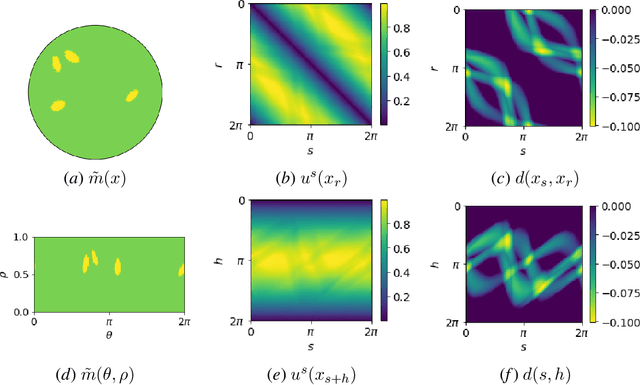
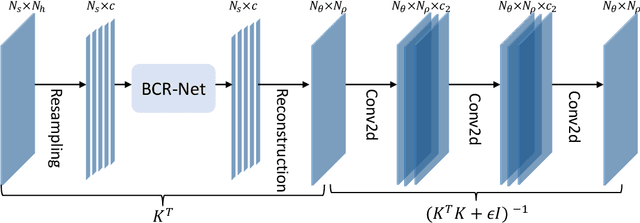
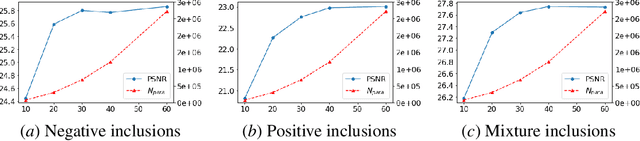
This paper introduces a neural network approach for solving two-dimensional traveltime tomography (TT) problems based on the eikonal equation. The mathematical problem of TT is to recover the slowness field of a medium based on the boundary measurement of the traveltimes of waves going through the medium. This inverse map is high-dimensional and nonlinear. For the circular tomography geometry, a perturbative analysis shows that the forward map can be approximated by a vectorized convolution operator in the angular direction. Motivated by this and filtered back-projection, we propose an effective neural network architecture for the inverse map using the recently proposed BCR-Net, with weights learned from training datasets. Numerical results demonstrate the efficiency of the proposed neural networks.

Solving Optical Tomography with Deep Learning

This paper presents a neural network approach for solving two-dimensional optical tomography (OT) problems based on the radiative transfer equation. The mathematical problem of OT is to recover the optical properties of an object based on the albedo operator that is accessible from boundary measurements. Both the forward map from the optical properties to the albedo operator and the inverse map are high-dimensional and nonlinear. For the circular tomography geometry, a perturbative analysis shows that the forward map can be approximated by a vectorized convolution operator in the angular direction. Motivated by this, we propose effective neural network architectures for the forward and inverse maps based on convolution layers, with weights learned from training datasets. Numerical results demonstrate the efficiency of the proposed neural networks.

Meta-learning Pseudo-differential Operators with Deep Neural Networks

This paper introduces a meta-learning approach for parameterized pseudo-differential operators with deep neural networks. With the help of the nonstandard wavelet form, the pseudo-differential operators can be approximated in a compressed form with a collection of vectors. The nonlinear map from the parameter to this collection of vectors and the wavelet transform are learned together from a small number of matrix-vector multiplications of the pseudo-differential operator. Numerical results for Green's functions of elliptic partial differential equations and the radiative transfer equations demonstrate the efficiency and accuracy of the proposed approach.

Solving Electrical Impedance Tomography with Deep Learning

This paper introduces a new approach for solving electrical impedance tomography (EIT) problems using deep neural networks. The mathematical problem of EIT is to invert the electrical conductivity from the Dirichlet-to-Neumann (DtN) map. Both the forward map from the electrical conductivity to the DtN map and the inverse map are high-dimensional and nonlinear. Motivated by the linear perturbative analysis of the forward map and based on a numerically low-rank property, we propose compact neural network architectures for the forward and inverse maps for both 2D and 3D problems. Numerical results demonstrate the efficiency of the proposed neural networks.

BCR-Net: a neural network based on the nonstandard wavelet form

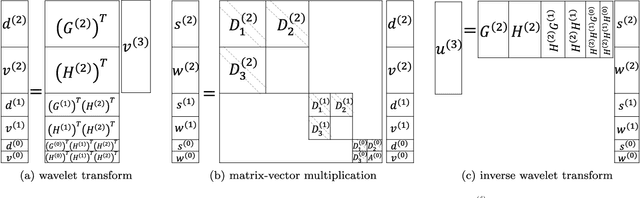
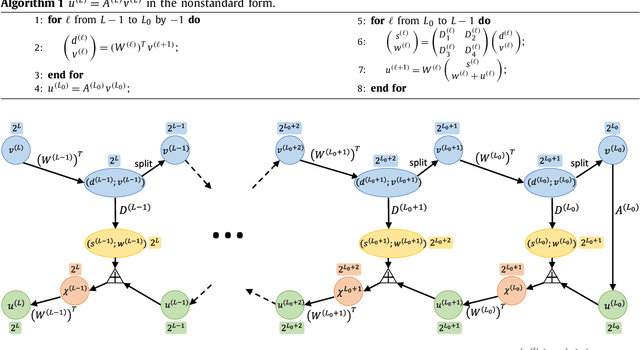
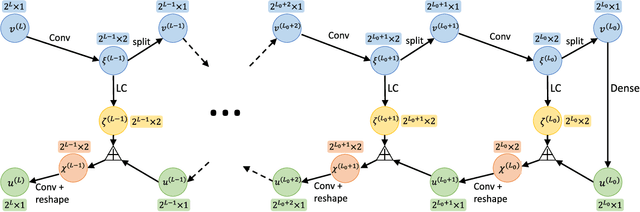
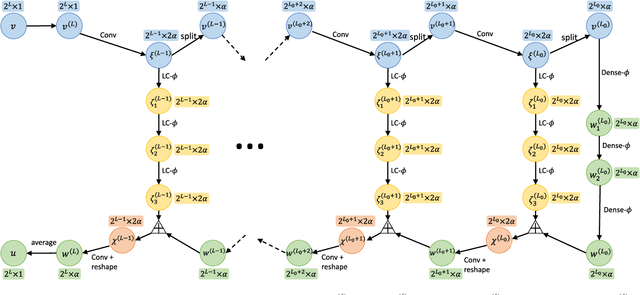
This paper proposes a novel neural network architecture inspired by the nonstandard form proposed by Beylkin, Coifman, and Rokhlin in [Communications on Pure and Applied Mathematics, 44(2), 141-183]. The nonstandard form is a highly effective wavelet-based compression scheme for linear integral operators. In this work, we first represent the matrix-vector product algorithm of the nonstandard form as a linear neural network where every scale of the multiresolution computation is carried out by a locally connected linear sub-network. In order to address nonlinear problems, we propose an extension, called BCR-Net, by replacing each linear sub-network with a deeper and more powerful nonlinear one. Numerical results demonstrate the efficiency of the new architecture by approximating nonlinear maps that arise in homogenization theory and stochastic computation.