BCR-Net: a neural network based on the nonstandard wavelet form
Paper and Code
Oct 20, 2018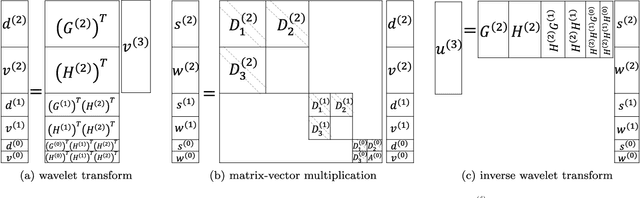
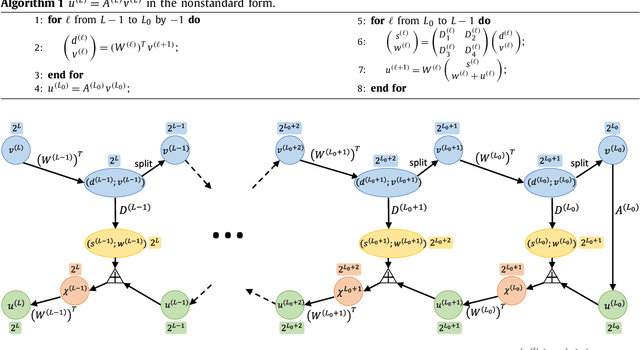
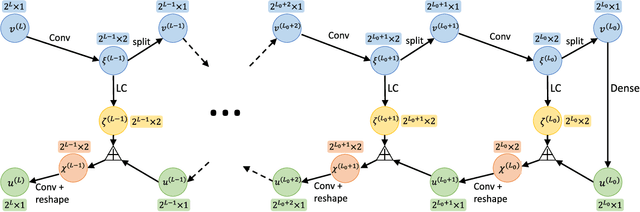
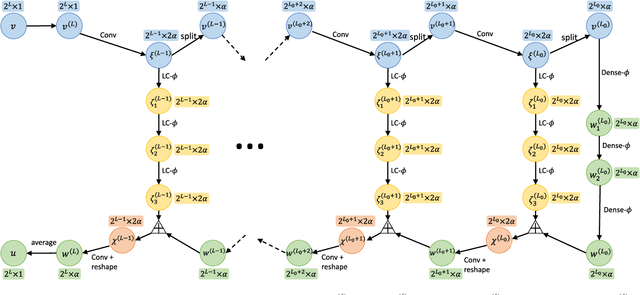
This paper proposes a novel neural network architecture inspired by the nonstandard form proposed by Beylkin, Coifman, and Rokhlin in [Communications on Pure and Applied Mathematics, 44(2), 141-183]. The nonstandard form is a highly effective wavelet-based compression scheme for linear integral operators. In this work, we first represent the matrix-vector product algorithm of the nonstandard form as a linear neural network where every scale of the multiresolution computation is carried out by a locally connected linear sub-network. In order to address nonlinear problems, we propose an extension, called BCR-Net, by replacing each linear sub-network with a deeper and more powerful nonlinear one. Numerical results demonstrate the efficiency of the new architecture by approximating nonlinear maps that arise in homogenization theory and stochastic computation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge