Matched Illumination

In previous work, it was shown that a camera can theoretically be made more colorimetric - its RGBs become more linearly related to XYZ tristimuli - by placing a specially designed color filter in the optical path. While the prior art demonstrated the principle, the optimal color-correction filters were not actually manufactured. In this paper, we provide a novel way of creating the color filtering effect without making a physical filter: we modulate the spectrum of the light source by using a spectrally tunable lighting system to recast the prefiltering effect from a lighting perspective. According to our method, if we wish to measure color under a D65 light, we relight the scene with a modulated D65 spectrum where the light modulation mimics the effect of color prefiltering in the prior art. We call our optimally modulated light, the matched illumination. In the experiments, using synthetic and real measurements, we show that color measurement errors can be reduced by about 50% or more on simulated data and 25% or more on real images when the matched illumination is used.

Mathematical derivation for Vora-Value based filter design method: Gradient and Hessian

In this paper, we present the detailed mathematical derivation of the gradient and Hessian matrix for the Vora-Value based colorimetric filter optimization. We make a full recapitulation of the steps involved in differentiating the objective function and reveal the positive-definite Hessian matrix when a positive regularizer is applied. This paper serves as a supplementary material for our paper in the colorimetric filter design theory.

Unifying Optimization Methods for Color Filter Design

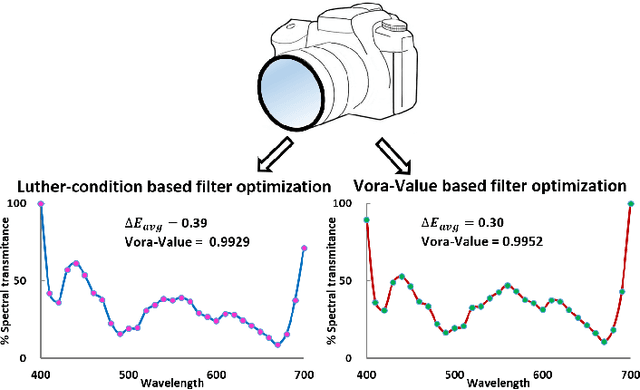
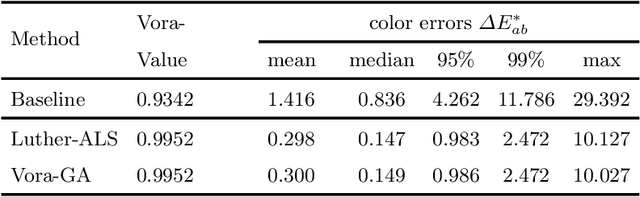
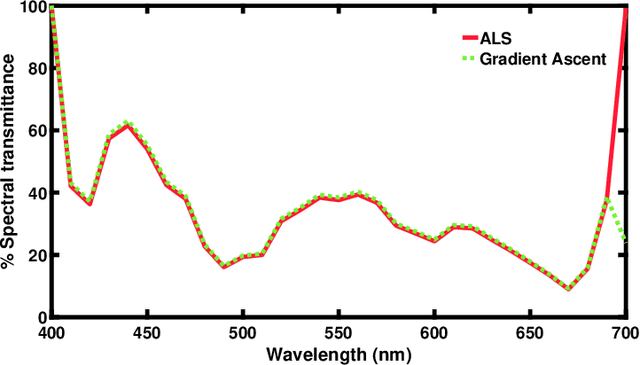
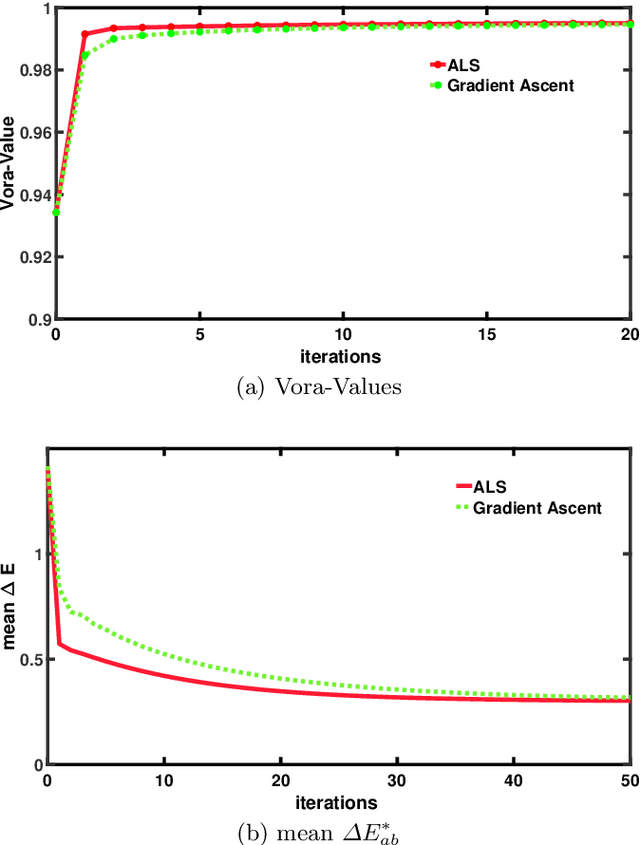
Through optimization we can solve for a filter that when the camera views the world through this filter, it is more colorimetric. Previous work solved for the filter that best satisfied the Luther condition: the camera spectral sensitivities after filtering were approximately a linear transform from the CIE XYZ color matching functions. A more recent method optimized for the filter that maximized the Vora-Value (a measure which relates to the closeness of the vector spaces spanned by the camera sensors and human vision sensors). The optimized Luther- and Vora-filters are different from one another. In this paper we begin by observing that the function defining the Vora-Value is equivalent to the Luther-condition optimization if we use the orthonormal basis of the XYZ color matching functions, i.e. we linearly transform the XYZ sensitivities to a set of orthonormal basis. In this formulation, the Luther-optimization algorithm is shown to almost optimize the Vora-Value. Moreover, experiments demonstrate that the modified orthonormal Luther-method finds the same color filter compared to the Vora-Value filter optimization. Significantly, our modified algorithm is simpler in formulation and also converges faster than the direct Vora-Value method.

Designing a Color Filter via Optimization of Vora-Value for Making a Camera more Colorimetric

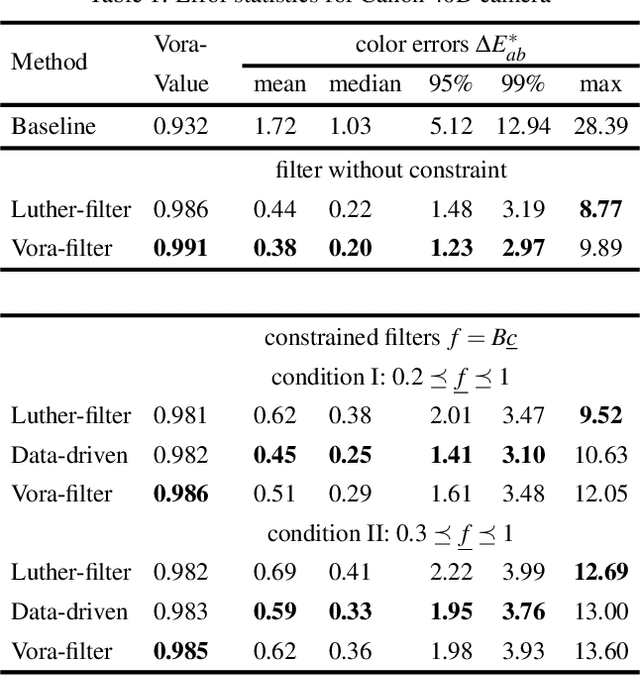
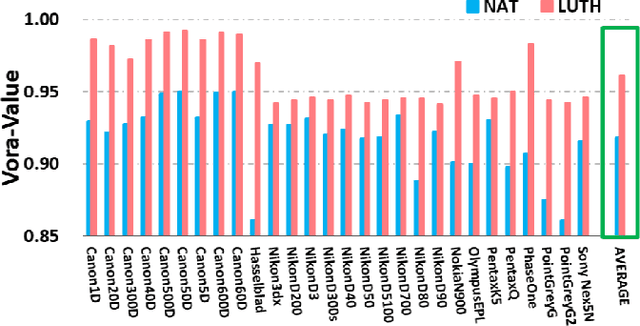
The Luther condition states that if the spectral sensitivity responses of a camera are a linear transform from the color matching functions of the human visual system, the camera is colorimetric. Previous work proposed to solve for a filter which, when placed in front of a camera, results in sensitivities that best satisfy the Luther condition. By construction, the prior art solves for a filter for a given set of human visual sensitivities, e.g. the XYZ color matching functions or the cone response functions. However, depending on the target spectral sensitivity set, a different optimal filter is found. This paper begins with the observation that the cone fundamentals, XYZ color matching functions or any linear combination thereof span the same 3-dimensional subspace. Thus, we set out to solve for a filter that makes the vector space spanned by the filtered camera sensitivities as similar as possible to the space spanned by human vision sensors. We argue that the Vora-Value is a suitable way to measure subspace similarity and we develop an optimization method for finding a filter that maximizes the Vora-Value measure. Experiments demonstrate that our new optimization leads to filtered camera sensitivities which have a significantly higher Vora-Value compared with antecedent methods.

Designing a physically-feasible colour filter to make a camera more colorimetric

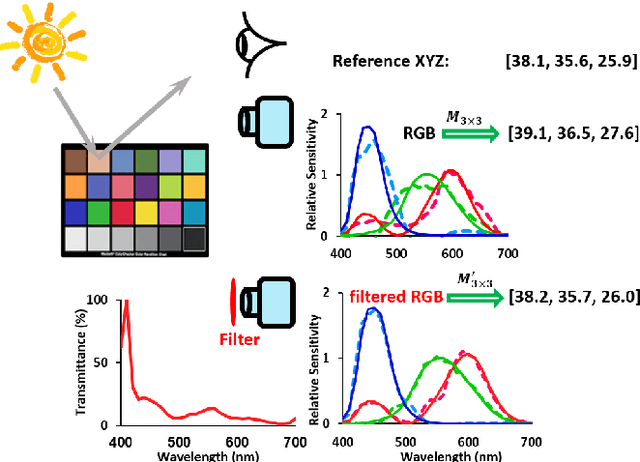
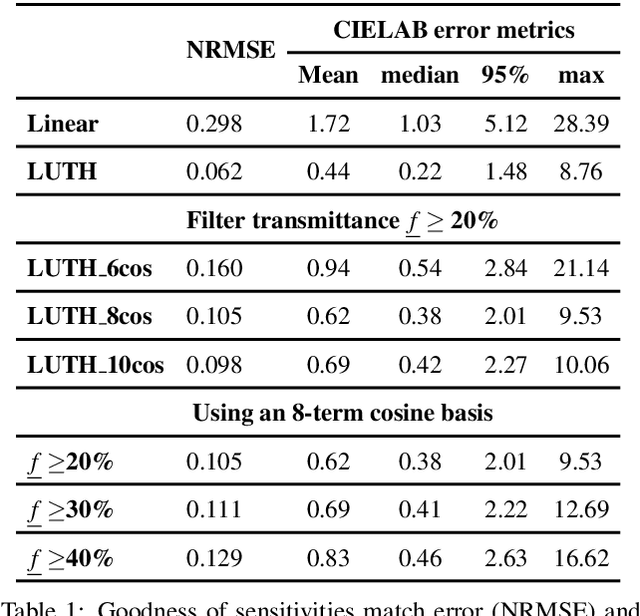
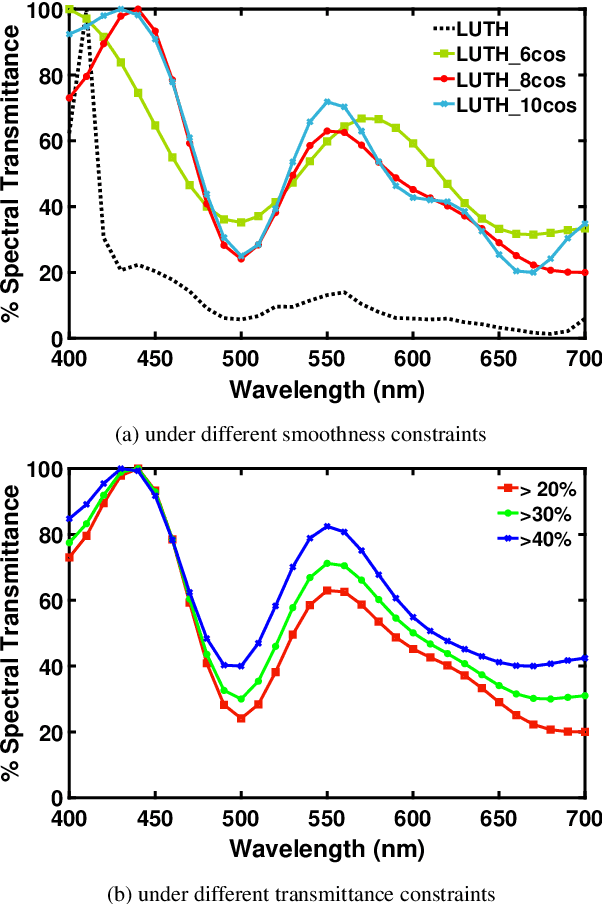
Previously, a method has been developed to find the best colour filter for a given camera which results in the new effective camera sensitivities that best meet the Luther condition. That is, the new sensitivities are approximately linearly related to the XYZ colour matching functions. However, with no constraint, the filter derived from this Luther-condition based optimisation can be rather non-smooth and transmit very little light which are impractical for fabrication. In this paper, we extend the Luther-condition filter optimisation method to allow us to incorporate both the smoothness and transmittance bounds of the recovered filter which are key practical concerns. Experiments demonstrate that we can find physically realisable filters which are smooth and reasonably transmissive with which the effective "camera+filter" becomes significantly more colorimetric.

Designing Color Filters that Make Cameras MoreColorimetric

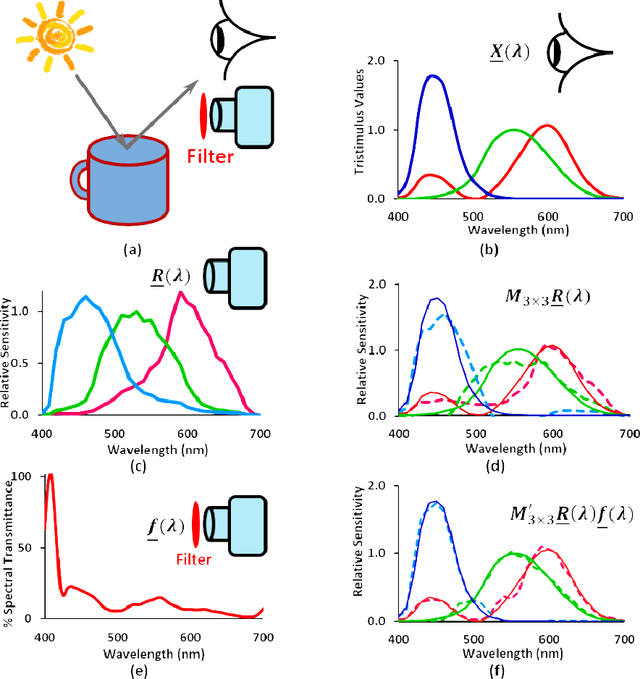
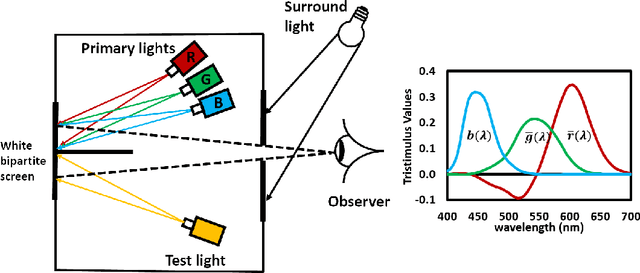
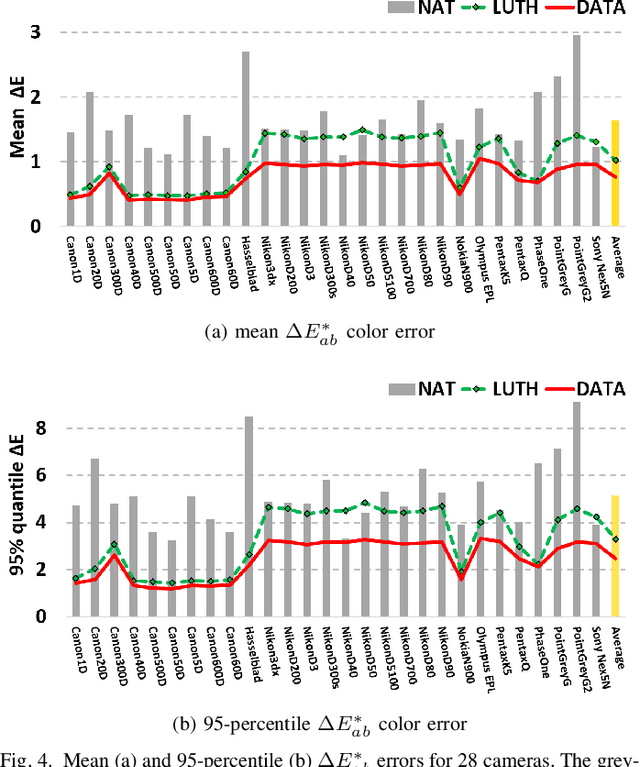
When we place a colored filter in front of a camera the effective camera response functions are equal to the given camera spectral sensitivities multiplied by the filter spectral transmittance. In this paper, we solve for the filter which returns the modified sensitivities as close to being a linear transformation from the color matching functions of human visual system as possible. When this linearity condition - sometimes called the Luther condition - is approximately met, the `camera+filter' system can be used for accurate color measurement. Then, we reformulate our filter design optimisation for making the sensor responses as close to the CIEXYZ tristimulus values as possible given the knowledge of real measured surfaces and illuminants spectra data. This data-driven method in turn is extended to incorporate constraints on the filter (smoothness and bounded transmission). Also, because how the optimisation is initialised is shown to impact on the performance of the solved-for filters, a multi-initialisation optimisation is developed. Experiments demonstrate that, by taking pictures through our optimised color filters we can make cameras significantly more colorimetric.