Designing a Color Filter via Optimization of Vora-Value for Making a Camera more Colorimetric
Paper and Code
May 13, 2020
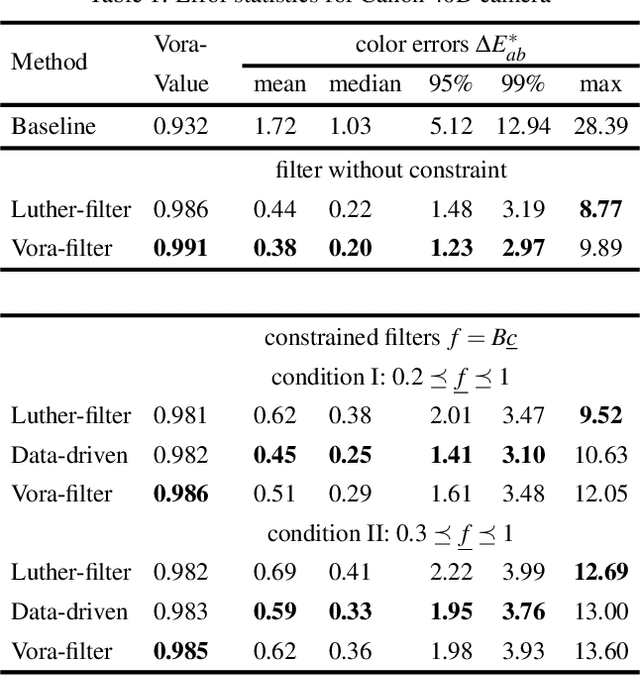

The Luther condition states that if the spectral sensitivity responses of a camera are a linear transform from the color matching functions of the human visual system, the camera is colorimetric. Previous work proposed to solve for a filter which, when placed in front of a camera, results in sensitivities that best satisfy the Luther condition. By construction, the prior art solves for a filter for a given set of human visual sensitivities, e.g. the XYZ color matching functions or the cone response functions. However, depending on the target spectral sensitivity set, a different optimal filter is found. This paper begins with the observation that the cone fundamentals, XYZ color matching functions or any linear combination thereof span the same 3-dimensional subspace. Thus, we set out to solve for a filter that makes the vector space spanned by the filtered camera sensitivities as similar as possible to the space spanned by human vision sensors. We argue that the Vora-Value is a suitable way to measure subspace similarity and we develop an optimization method for finding a filter that maximizes the Vora-Value measure. Experiments demonstrate that our new optimization leads to filtered camera sensitivities which have a significantly higher Vora-Value compared with antecedent methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge