Neural Fourier Modelling: A Highly Compact Approach to Time-Series Analysis

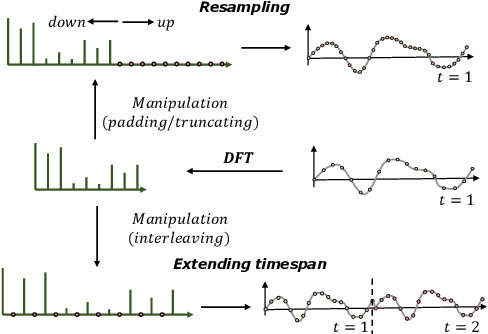
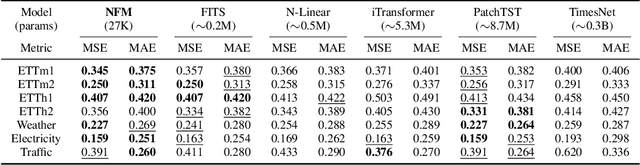
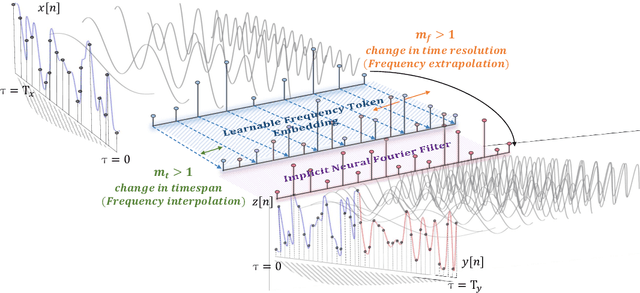
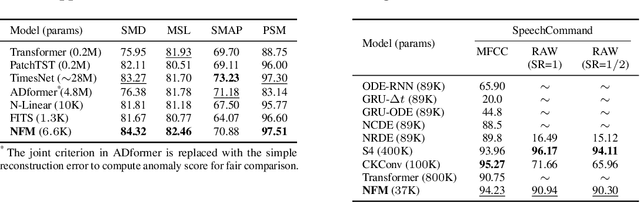
Neural time-series analysis has traditionally focused on modeling data in the time domain, often with some approaches incorporating equivalent Fourier domain representations as auxiliary spectral features. In this work, we shift the main focus to frequency representations, modeling time-series data fully and directly in the Fourier domain. We introduce Neural Fourier Modelling (NFM), a compact yet powerful solution for time-series analysis. NFM is grounded in two key properties of the Fourier transform (FT): (i) the ability to model finite-length time series as functions in the Fourier domain, treating them as continuous-time elements in function space, and (ii) the capacity for data manipulation (such as resampling and timespan extension) within the Fourier domain. We reinterpret Fourier-domain data manipulation as frequency extrapolation and interpolation, incorporating this as a core learning mechanism in NFM, applicable across various tasks. To support flexible frequency extension with spectral priors and effective modulation of frequency representations, we propose two learning modules: Learnable Frequency Tokens (LFT) and Implicit Neural Fourier Filters (INFF). These modules enable compact and expressive modeling in the Fourier domain. Extensive experiments demonstrate that NFM achieves state-of-the-art performance on a wide range of tasks (forecasting, anomaly detection, and classification), including challenging time-series scenarios with previously unseen sampling rates at test time. Moreover, NFM is highly compact, requiring fewer than 40K parameters in each task, with time-series lengths ranging from 100 to 16K.

DNN-based Source Enhancement to Increase Objective Sound Quality Assessment Score

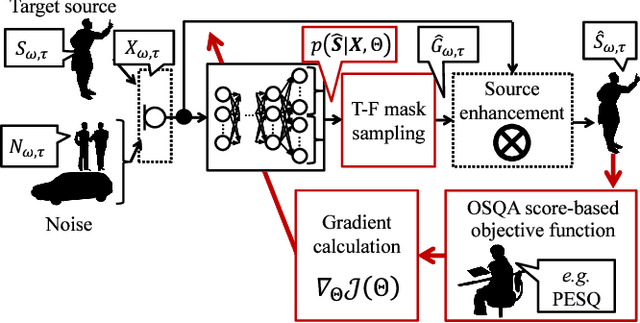
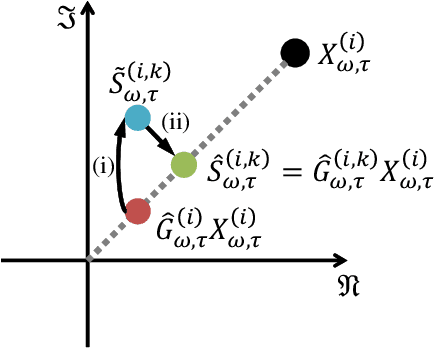
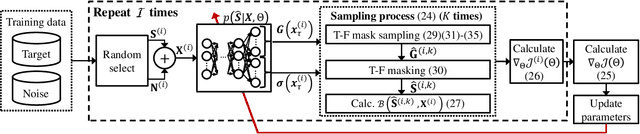
We propose a training method for deep neural network (DNN)-based source enhancement to increase objective sound quality assessment (OSQA) scores such as the perceptual evaluation of speech quality (PESQ). In many conventional studies, DNNs have been used as a mapping function to estimate time-frequency masks and trained to minimize an analytically tractable objective function such as the mean squared error (MSE). Since OSQA scores have been used widely for sound-quality evaluation, constructing DNNs to increase OSQA scores would be better than using the minimum-MSE to create high-quality output signals. However, since most OSQA scores are not analytically tractable, \textit{i.e.}, they are black boxes, the gradient of the objective function cannot be calculated by simply applying back-propagation. To calculate the gradient of the OSQA-based objective function, we formulated a DNN optimization scheme on the basis of \textit{black-box optimization}, which is used for training a computer that plays a game. For a black-box-optimization scheme, we adopt the policy gradient method for calculating the gradient on the basis of a sampling algorithm. To simulate output signals using the sampling algorithm, DNNs are used to estimate the probability density function of the output signals that maximize OSQA scores. The OSQA scores are calculated from the simulated output signals, and the DNNs are trained to increase the probability of generating the simulated output signals that achieve high OSQA scores. Through several experiments, we found that OSQA scores significantly increased by applying the proposed method, even though the MSE was not minimized.