Mini-Hes: A Parallelizable Second-order Latent Factor Analysis Model

Interactions among large number of entities is naturally high-dimensional and incomplete (HDI) in many big data related tasks. Behavioral characteristics of users are hidden in these interactions, hence, effective representation of the HDI data is a fundamental task for understanding user behaviors. Latent factor analysis (LFA) model has proven to be effective in representing HDI data. The performance of an LFA model relies heavily on its training process, which is a non-convex optimization. It has been proven that incorporating local curvature and preprocessing gradients during its training process can lead to superior performance compared to LFA models built with first-order family methods. However, with the escalation of data volume, the feasibility of second-order algorithms encounters challenges. To address this pivotal issue, this paper proposes a mini-block diagonal hessian-free (Mini-Hes) optimization for building an LFA model. It leverages the dominant diagonal blocks in the generalized Gauss-Newton matrix based on the analysis of the Hessian matrix of LFA model and serves as an intermediary strategy bridging the gap between first-order and second-order optimization methods. Experiment results indicate that, with Mini-Hes, the LFA model outperforms several state-of-the-art models in addressing missing data estimation task on multiple real HDI datasets from recommender system. (The source code of Mini-Hes is available at https://github.com/Goallow/Mini-Hes)

A Dynamic Linear Bias Incorporation Scheme for Nonnegative Latent Factor Analysis

High-Dimensional and Incomplete (HDI) data is commonly encountered in big data-related applications like social network services systems, which are concerning the limited interactions among numerous nodes. Knowledge acquisition from HDI data is a vital issue in the domain of data science due to their embedded rich patterns like node behaviors, where the fundamental task is to perform HDI data representation learning. Nonnegative Latent Factor Analysis (NLFA) models have proven to possess the superiority to address this issue, where a linear bias incorporation (LBI) scheme is important in present the training overshooting and fluctuation, as well as preventing the model from premature convergence. However, existing LBI schemes are all statistic ones where the linear biases are fixed, which significantly restricts the scalability of the resultant NLFA model and results in loss of representation learning ability to HDI data. Motivated by the above discoveries, this paper innovatively presents the dynamic linear bias incorporation (DLBI) scheme. It firstly extends the linear bias vectors into matrices, and then builds a binary weight matrix to switch the active/inactive states of the linear biases. The weight matrix's each entry switches between the binary states dynamically corresponding to the linear bias value variation, thereby establishing the dynamic linear biases for an NLFA model. Empirical studies on three HDI datasets from real applications demonstrate that the proposed DLBI-based NLFA model obtains higher representation accuracy several than state-of-the-art models do, as well as highly-competitive computational efficiency.

Multi-constrained Symmetric Nonnegative Latent Factor Analysis for Accurately Representing Large-scale Undirected Weighted Networks

An Undirected Weighted Network (UWN) is frequently encountered in a big-data-related application concerning the complex interactions among numerous nodes, e.g., a protein interaction network from a bioinformatics application. A Symmetric High-Dimensional and Incomplete (SHDI) matrix can smoothly illustrate such an UWN, which contains rich knowledge like node interaction behaviors and local complexes. To extract desired knowledge from an SHDI matrix, an analysis model should carefully consider its symmetric-topology for describing an UWN's intrinsic symmetry. Representation learning to an UWN borrows the success of a pyramid of symmetry-aware models like a Symmetric Nonnegative Matrix Factorization (SNMF) model whose objective function utilizes a sole Latent Factor (LF) matrix for representing SHDI's symmetry rigorously. However, they suffer from the following drawbacks: 1) their computational complexity is high; and 2) their modeling strategy narrows their representation features, making them suffer from low learning ability. Aiming at addressing above critical issues, this paper proposes a Multi-constrained Symmetric Nonnegative Latent-factor-analysis (MSNL) model with two-fold ideas: 1) introducing multi-constraints composed of multiple LF matrices, i.e., inequality and equality ones into a data-density-oriented objective function for precisely representing the intrinsic symmetry of an SHDI matrix with broadened feature space; and 2) implementing an Alternating Direction Method of Multipliers (ADMM)-incorporated learning scheme for precisely solving such a multi-constrained model. Empirical studies on three SHDI matrices from a real bioinformatics or industrial application demonstrate that the proposed MSNL model achieves stronger representation learning ability to an SHDI matrix than state-of-the-art models do.

Proximal Symmetric Non-negative Latent Factor Analysis: A Novel Approach to Highly-Accurate Representation of Undirected Weighted Networks

An Undirected Weighted Network (UWN) is commonly found in big data-related applications. Note that such a network's information connected with its nodes, and edges can be expressed as a Symmetric, High-Dimensional and Incomplete (SHDI) matrix. However, existing models fail in either modeling its intrinsic symmetry or low-data density, resulting in low model scalability or representation learning ability. For addressing this issue, a Proximal Symmetric Nonnegative Latent-factor-analysis (PSNL) model is proposed. It incorporates a proximal term into symmetry-aware and data density-oriented objective function for high representation accuracy. Then an adaptive Alternating Direction Method of Multipliers (ADMM)-based learning scheme is implemented through a Tree-structured of Parzen Estimators (TPE) method for high computational efficiency. Empirical studies on four UWNs demonstrate that PSNL achieves higher accuracy gain than state-of-the-art models, as well as highly competitive computational efficiency.

A Practical Second-order Latent Factor Model via Distributed Particle Swarm Optimization

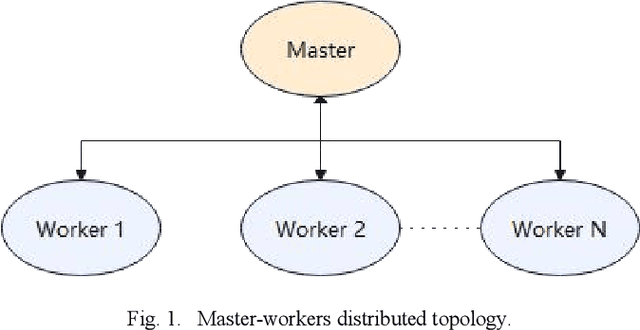
Latent Factor (LF) models are effective in representing high-dimension and sparse (HiDS) data via low-rank matrices approximation. Hessian-free (HF) optimization is an efficient method to utilizing second-order information of an LF model's objective function and it has been utilized to optimize second-order LF (SLF) model. However, the low-rank representation ability of a SLF model heavily relies on its multiple hyperparameters. Determining these hyperparameters is time-consuming and it largely reduces the practicability of an SLF model. To address this issue, a practical SLF (PSLF) model is proposed in this work. It realizes hyperparameter self-adaptation with a distributed particle swarm optimizer (DPSO), which is gradient-free and parallelized. Experiments on real HiDS data sets indicate that PSLF model has a competitive advantage over state-of-the-art models in data representation ability.

An Unconstrained Symmetric Nonnegative Latent Factor Analysis for Large-scale Undirected Weighted Networks

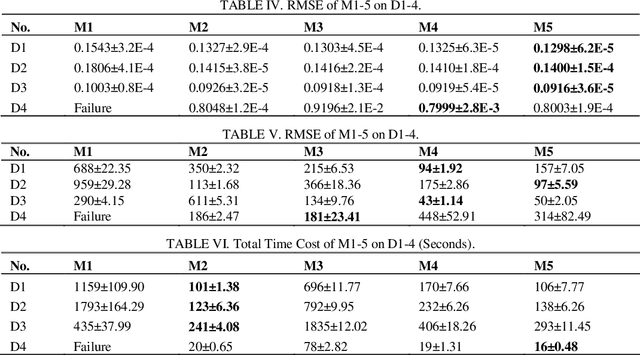
Large-scale undirected weighted networks are usually found in big data-related research fields. It can naturally be quantified as a symmetric high-dimensional and incomplete (SHDI) matrix for implementing big data analysis tasks. A symmetric non-negative latent-factor-analysis (SNL) model is able to efficiently extract latent factors (LFs) from an SHDI matrix. Yet it relies on a constraint-combination training scheme, which makes it lack flexibility. To address this issue, this paper proposes an unconstrained symmetric nonnegative latent-factor-analysis (USNL) model. Its main idea is two-fold: 1) The output LFs are separated from the decision parameters via integrating a nonnegative mapping function into an SNL model; and 2) Stochastic gradient descent (SGD) is adopted for implementing unconstrained model training along with ensuring the output LFs nonnegativity. Empirical studies on four SHDI matrices generated from real big data applications demonstrate that an USNL model achieves higher prediction accuracy of missing data than an SNL model, as well as highly competitive computational efficiency.

An Adaptive Alternating-direction-method-based Nonnegative Latent Factor Model

An alternating-direction-method-based nonnegative latent factor model can perform efficient representation learning to a high-dimensional and incomplete (HDI) matrix. However, it introduces multiple hyper-parameters into the learning process, which should be chosen with care to enable its superior performance. Its hyper-parameter adaptation is desired for further enhancing its scalability. Targeting at this issue, this paper proposes an Adaptive Alternating-direction-method-based Nonnegative Latent Factor (A2NLF) model, whose hyper-parameter adaptation is implemented following the principle of particle swarm optimization. Empirical studies on nonnegative HDI matrices generated by industrial applications indicate that A2NLF outperforms several state-of-the-art models in terms of computational and storage efficiency, as well as maintains highly competitive estimation accuracy for an HDI matrix's missing data.