An Unconstrained Symmetric Nonnegative Latent Factor Analysis for Large-scale Undirected Weighted Networks

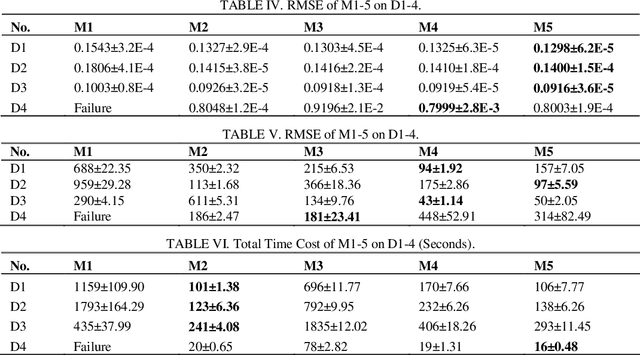
Large-scale undirected weighted networks are usually found in big data-related research fields. It can naturally be quantified as a symmetric high-dimensional and incomplete (SHDI) matrix for implementing big data analysis tasks. A symmetric non-negative latent-factor-analysis (SNL) model is able to efficiently extract latent factors (LFs) from an SHDI matrix. Yet it relies on a constraint-combination training scheme, which makes it lack flexibility. To address this issue, this paper proposes an unconstrained symmetric nonnegative latent-factor-analysis (USNL) model. Its main idea is two-fold: 1) The output LFs are separated from the decision parameters via integrating a nonnegative mapping function into an SNL model; and 2) Stochastic gradient descent (SGD) is adopted for implementing unconstrained model training along with ensuring the output LFs nonnegativity. Empirical studies on four SHDI matrices generated from real big data applications demonstrate that an USNL model achieves higher prediction accuracy of missing data than an SNL model, as well as highly competitive computational efficiency.