Aggregating Algorithm for Prediction of Packs

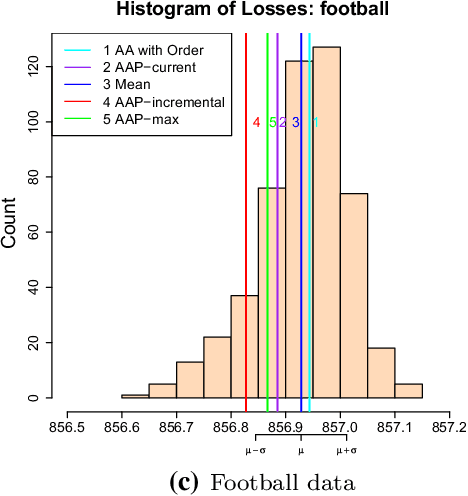
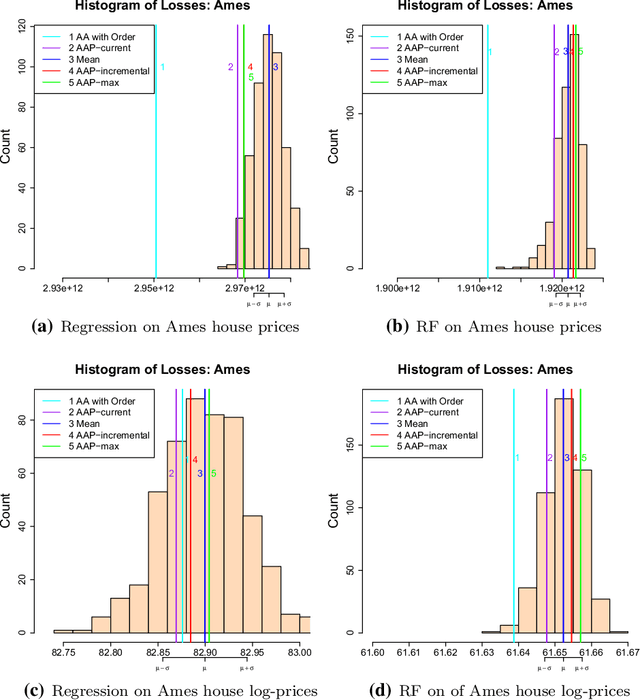
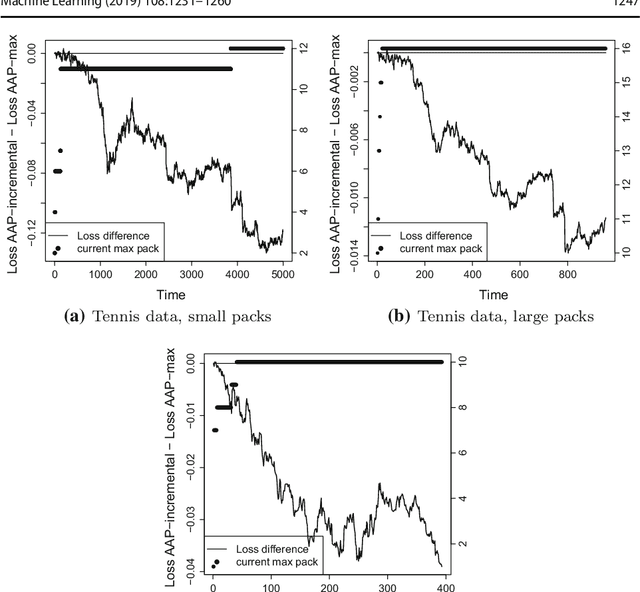
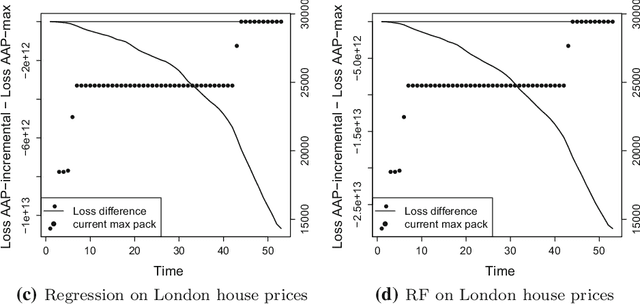
This paper formulates the protocol for prediction of packs, which a special case of prediction under delayed feedback. Under this protocol, the learner must make a few predictions without seeing the outcomes and then the outcomes are revealed. We develop the theory of prediction with expert advice for packs. By applying Vovk's Aggregating Algorithm to this problem we obtain a number of algorithms with tight upper bounds. We carry out empirical experiments on housing data.

On-line Prediction with Kernels and the Complexity Approximation Principle

The paper describes an application of Aggregating Algorithm to the problem of regression. It generalizes earlier results concerned with plain linear regression to kernel techniques and presents an on-line algorithm which performs nearly as well as any oblivious kernel predictor. The paper contains the derivation of an estimate on the performance of this algorithm. The estimate is then used to derive an application of the Complexity Approximation Principle to kernel methods.

An Identity for Kernel Ridge Regression

This paper derives an identity connecting the square loss of ridge regression in on-line mode with the loss of the retrospectively best regressor. Some corollaries about the properties of the cumulative loss of on-line ridge regression are also obtained.

Supermartingales in Prediction with Expert Advice

We apply the method of defensive forecasting, based on the use of game-theoretic supermartingales, to prediction with expert advice. In the traditional setting of a countable number of experts and a finite number of outcomes, the Defensive Forecasting Algorithm is very close to the well-known Aggregating Algorithm. Not only the performance guarantees but also the predictions are the same for these two methods of fundamentally different nature. We discuss also a new setting where the experts can give advice conditional on the learner's future decision. Both the algorithms can be adapted to the new setting and give the same performance guarantees as in the traditional setting. Finally, we outline an application of defensive forecasting to a setting with several loss functions.

Aggregating Algorithm competing with Banach lattices

The paper deals with on-line regression settings with signals belonging to a Banach lattice. Our algorithms work in a semi-online setting where all the inputs are known in advance and outcomes are unknown and given step by step. We apply the Aggregating Algorithm to construct a prediction method whose cumulative loss over all the input vectors is comparable with the cumulative loss of any linear functional on the Banach lattice. As a by-product we get an algorithm that takes signals from an arbitrary domain. Its cumulative loss is comparable with the cumulative loss of any predictor function from Besov and Triebel-Lizorkin spaces. We describe several applications of our setting.

Linear Probability Forecasting

Multi-class classification is one of the most important tasks in machine learning. In this paper we consider two online multi-class classification problems: classification by a linear model and by a kernelized model. The quality of predictions is measured by the Brier loss function. We suggest two computationally efficient algorithms to work with these problems and prove theoretical guarantees on their losses. We kernelize one of the algorithms and prove theoretical guarantees on its loss. We perform experiments and compare our algorithms with logistic regression.