Guidance algorithm for smooth trajectory tracking of a fixed wing UAV flying in wind flows

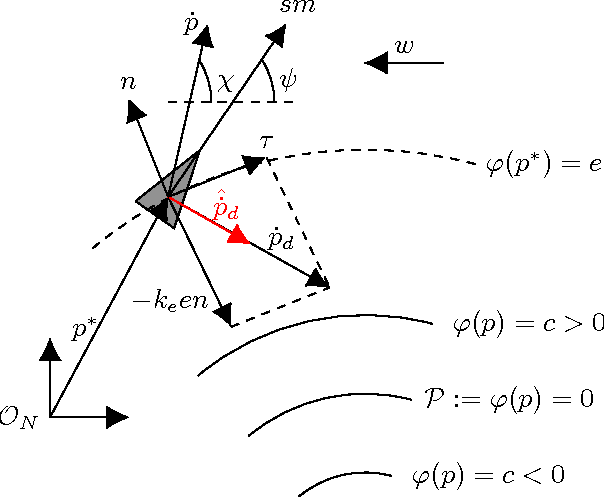
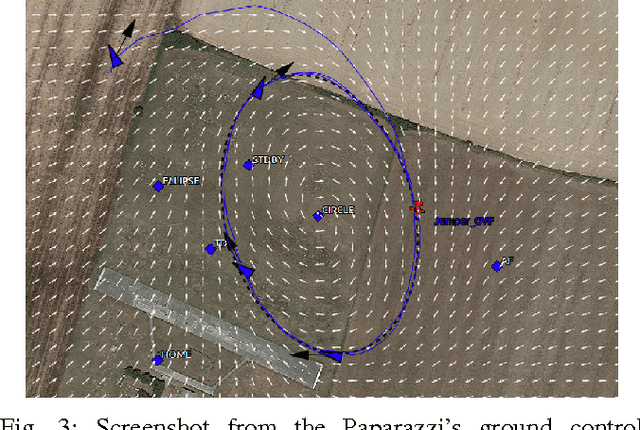
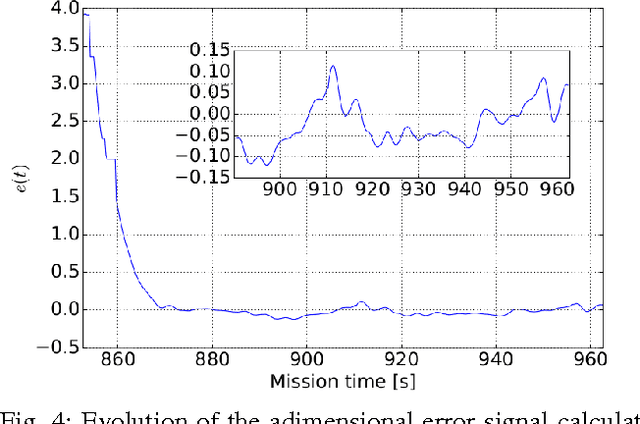
This paper presents an algorithm for solving the problem of tracking smooth curves by a fixed wing unmanned aerial vehicle travelling with a constant airspeed and under a constant wind disturbance. The algorithm is based on the idea of following a guiding vector field which is constructed from the implicit function that describes the desired (possibly time-varying) trajectory. The output of the algorithm can be directly expressed in terms of the bank angle of the UAV in order to achieve coordinated turns. Furthermore, the algorithm can be tuned offline such that physical constraints of the UAV, e.g. the maximum bank angle, will not be violated in a neighborhood of the desired trajectory. We provide the corresponding theoretical convergence analysis and performance results from actual flights.

A guiding vector field algorithm for path following control of nonholonomic mobile robots

In this paper we propose an algorithm for path following control of the nonholonomic mobile robot based on the idea of the guiding vector field (GVF). The desired path may be an arbitrary smooth curve in its implicit form, that is, a level set of a predefined smooth function. Using this function and the robot's kinematic model, we design a GVF, whose integral curves converge to the trajectory. A nonlinear motion controller is then proposed which steers the robot along such an integral curve, bringing it to the desired path. We establish global convergence conditions for our algorithm and demonstrate its applicability and performance by experiments with real wheeled robots.