Analysis of Higher-Order Ising Hamiltonians

It is challenging to scale Ising machines for industrial-level problems due to algorithm or hardware limitations. Although higher-order Ising models provide a more compact encoding, they are, however, hard to physically implement. This work proposes a theoretical framework of a higher-order Ising simulator, IsingSim. The Ising spins and gradients in IsingSim are decoupled and self-customizable. We significantly accelerate the simulation speed via a bidirectional approach for differentiating the hyperedge functions. Our proof-of-concept implementation verifies the theoretical framework by simulating the Ising spins with exact and approximate gradients. Experiment results show that our novel framework can be a useful tool for providing design guidelines for higher-order Ising machines.

Massively Parallel Continuous Local Search for Hybrid SAT Solving on GPUs

Although state-of-the-art (SOTA) SAT solvers based on conflict-driven clause learning (CDCL) have achieved remarkable engineering success, their sequential nature limits the parallelism that may be extracted for acceleration on platforms such as the graphics processing unit (GPU). In this work, we propose FastFourierSAT, a highly parallel hybrid SAT solver based on gradient-driven continuous local search (CLS). This is realized by a novel parallel algorithm inspired by the Fast Fourier Transform (FFT)-based convolution for computing the elementary symmetric polynomials (ESPs), which is the major computational task in previous CLS methods. The complexity of our algorithm matches the best previous result. Furthermore, the substantial parallelism inherent in our algorithm can leverage the GPU for acceleration, demonstrating significant improvement over the previous CLS approaches. We also propose to incorporate the restart heuristics in CLS to improve search efficiency. We compare our approach with the SOTA parallel SAT solvers on several benchmarks. Our results show that FastFourierSAT computes the gradient 100+ times faster than previous prototypes implemented on CPU. Moreover, FastFourierSAT solves most instances and demonstrates promising performance on larger-size instances.

CITS: Coherent Ising Tree Search Algorithm Towards Solving Combinatorial Optimization Problems

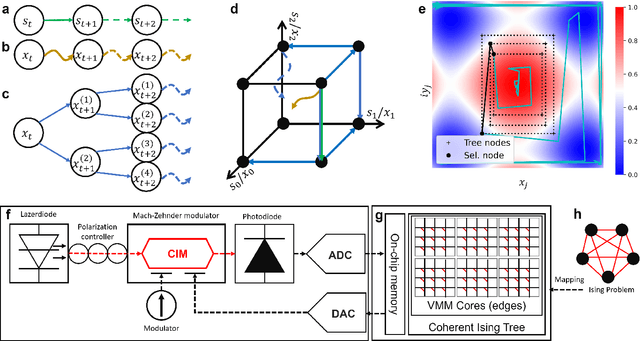
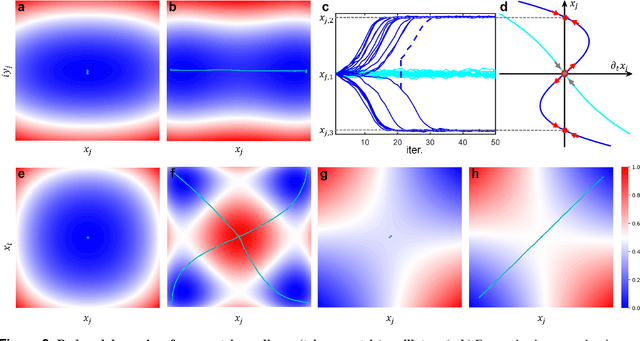
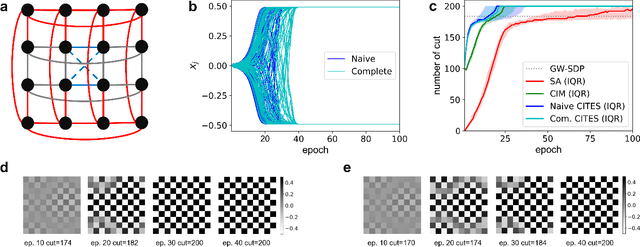
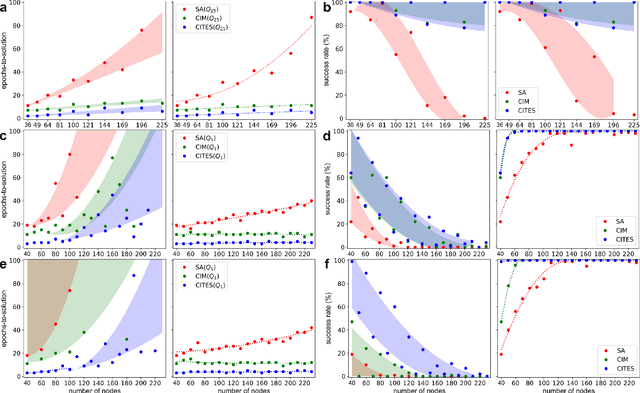
Simulated annealing (SA) attracts more attention among classical heuristic algorithms because the solution of the combinatorial optimization problem can be naturally mapped to the ground state of the Ising Hamiltonian. However, in practical implementation, the annealing process cannot be arbitrarily slow and hence, it may deviate from the expected stationary Boltzmann distribution and become trapped in a local energy minimum. To overcome this problem, this paper proposes a heuristic search algorithm by expanding search space from a Markov chain to a recursive depth limited tree based on SA, where the parent and child nodes represent the current and future spin states. At each iteration, the algorithm will select the best near-optimal solution within the feasible search space by exploring along the tree in the sense of `look ahead'. Furthermore, motivated by coherent Ising machine (CIM), we relax the discrete representation of spin states to continuous representation with a regularization term and utilize the reduced dynamics of the oscillators to explore the surrounding neighborhood of the selected tree nodes. We tested our algorithm on a representative NP-hard problem (MAX-CUT) to illustrate the effectiveness of this algorithm compared to semi-definite programming (SDP), SA, and simulated CIM. Our results show that above the primal heuristics SA and CIM, our high-level tree search strategy is able to provide solutions within fewer epochs for Ising formulated NP-optimization problems.