CITS: Coherent Ising Tree Search Algorithm Towards Solving Combinatorial Optimization Problems
Paper and Code
Mar 09, 2022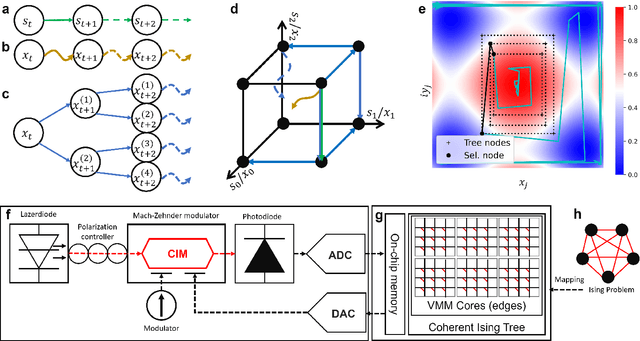
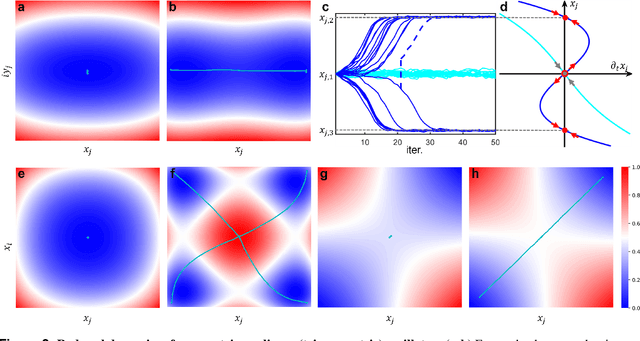
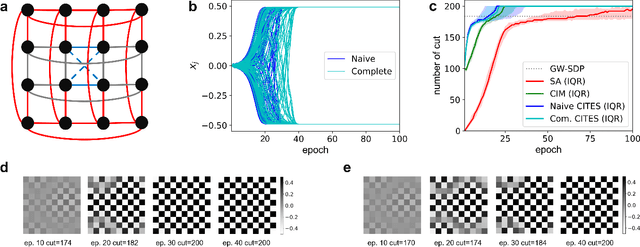
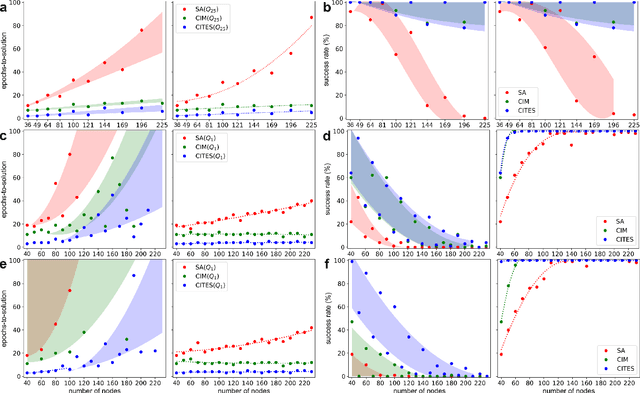
Simulated annealing (SA) attracts more attention among classical heuristic algorithms because the solution of the combinatorial optimization problem can be naturally mapped to the ground state of the Ising Hamiltonian. However, in practical implementation, the annealing process cannot be arbitrarily slow and hence, it may deviate from the expected stationary Boltzmann distribution and become trapped in a local energy minimum. To overcome this problem, this paper proposes a heuristic search algorithm by expanding search space from a Markov chain to a recursive depth limited tree based on SA, where the parent and child nodes represent the current and future spin states. At each iteration, the algorithm will select the best near-optimal solution within the feasible search space by exploring along the tree in the sense of `look ahead'. Furthermore, motivated by coherent Ising machine (CIM), we relax the discrete representation of spin states to continuous representation with a regularization term and utilize the reduced dynamics of the oscillators to explore the surrounding neighborhood of the selected tree nodes. We tested our algorithm on a representative NP-hard problem (MAX-CUT) to illustrate the effectiveness of this algorithm compared to semi-definite programming (SDP), SA, and simulated CIM. Our results show that above the primal heuristics SA and CIM, our high-level tree search strategy is able to provide solutions within fewer epochs for Ising formulated NP-optimization problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge