AlphaRouter: Quantum Circuit Routing with Reinforcement Learning and Tree Search

Quantum computers have the potential to outperform classical computers in important tasks such as optimization and number factoring. They are characterized by limited connectivity, which necessitates the routing of their computational bits, known as qubits, to specific locations during program execution to carry out quantum operations. Traditionally, the NP-hard optimization problem of minimizing the routing overhead has been addressed through sub-optimal rule-based routing techniques with inherent human biases embedded within the cost function design. This paper introduces a solution that integrates Monte Carlo Tree Search (MCTS) with Reinforcement Learning (RL). Our RL-based router, called AlphaRouter, outperforms the current state-of-the-art routing methods and generates quantum programs with up to $20\%$ less routing overhead, thus significantly enhancing the overall efficiency and feasibility of quantum computing.

Élivágar: Efficient Quantum Circuit Search for Classification

Designing performant and noise-robust circuits for Quantum Machine Learning (QML) is challenging -- the design space scales exponentially with circuit size, and there are few well-supported guiding principles for QML circuit design. Although recent Quantum Circuit Search (QCS) methods attempt to search for performant QML circuits that are also robust to hardware noise, they directly adopt designs from classical Neural Architecture Search (NAS) that are misaligned with the unique constraints of quantum hardware, resulting in high search overheads and severe performance bottlenecks. We present \'Eliv\'agar, a novel resource-efficient, noise-guided QCS framework. \'Eliv\'agar innovates in all three major aspects of QCS -- search space, search algorithm and candidate evaluation strategy -- to address the design flaws in current classically-inspired QCS methods. \'Eliv\'agar achieves hardware-efficiency and avoids an expensive circuit-mapping co-search via noise- and device topology-aware candidate generation. By introducing two cheap-to-compute predictors, Clifford noise resilience and Representational capacity, \'Eliv\'agar decouples the evaluation of noise robustness and performance, enabling early rejection of low-fidelity circuits and reducing circuit evaluation costs. Due to its resource-efficiency, \'Eliv\'agar can further search for data embeddings, significantly improving performance. Based on a comprehensive evaluation of \'Eliv\'agar on 12 real quantum devices and 9 QML applications, \'Eliv\'agar achieves 5.3% higher accuracy and a 271$\times$ speedup compared to state-of-the-art QCS methods.

Optimized Compilation of Aggregated Instructions for Realistic Quantum Computers

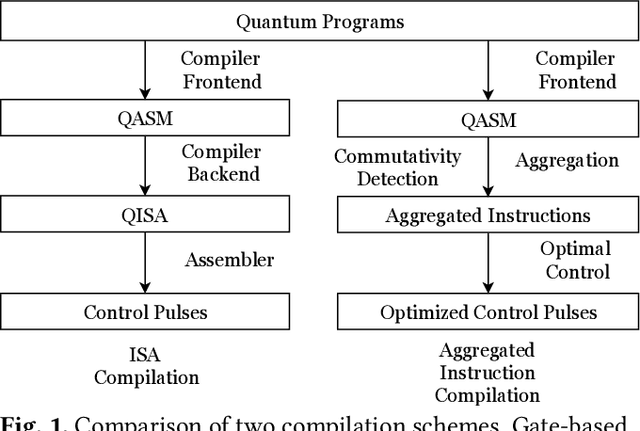
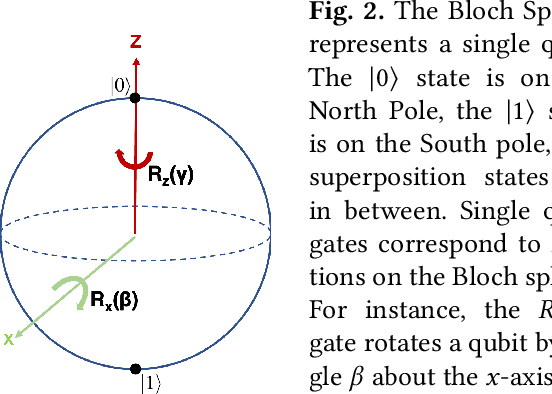
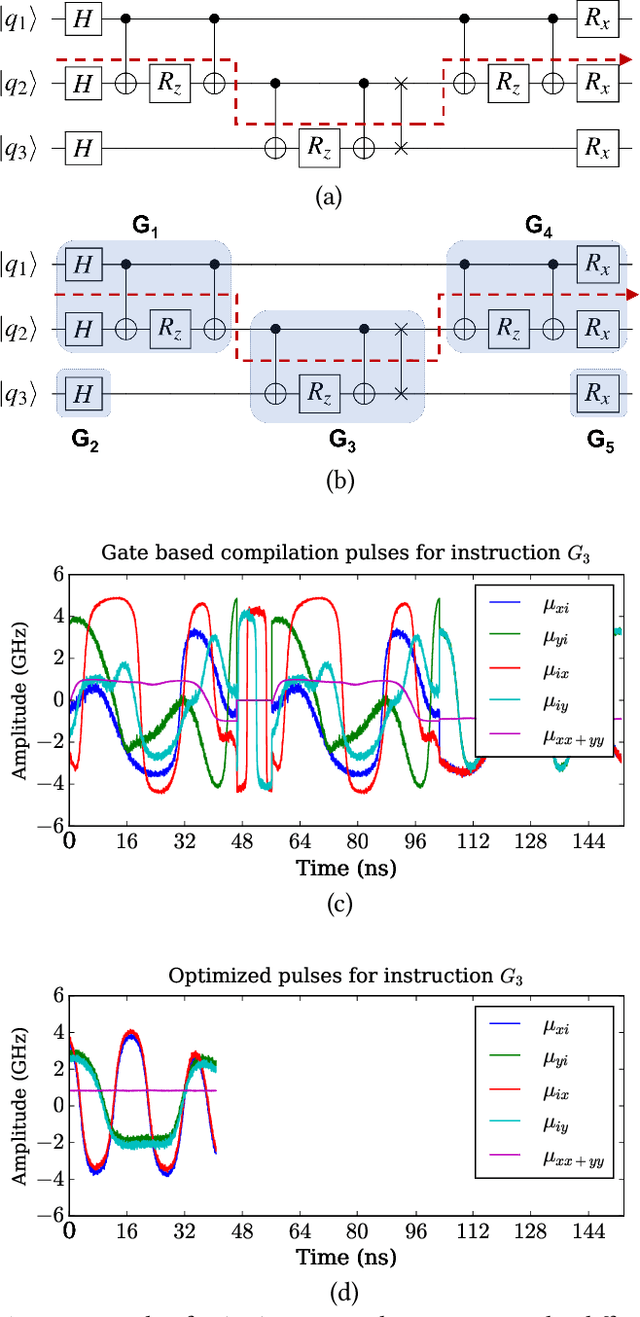
Recent developments in engineering and algorithms have made real-world applications in quantum computing possible in the near future. Existing quantum programming languages and compilers use a quantum assembly language composed of 1- and 2-qubit (quantum bit) gates. Quantum compiler frameworks translate this quantum assembly to electric signals (called control pulses) that implement the specified computation on specific physical devices. However, there is a mismatch between the operations defined by the 1- and 2-qubit logical ISA and their underlying physical implementation, so the current practice of directly translating logical instructions into control pulses results in inefficient, high-latency programs. To address this inefficiency, we propose a universal quantum compilation methodology that aggregates multiple logical operations into larger units that manipulate up to 10 qubits at a time. Our methodology then optimizes these aggregates by (1) finding commutative intermediate operations that result in more efficient schedules and (2) creating custom control pulses optimized for the aggregate (instead of individual 1- and 2-qubit operations). Compared to the standard gate-based compilation, the proposed approach realizes a deeper vertical integration of high-level quantum software and low-level, physical quantum hardware. We evaluate our approach on important near-term quantum applications on simulations of superconducting quantum architectures. Our proposed approach provides a mean speedup of $5\times$, with a maximum of $10\times$. Because latency directly affects the feasibility of quantum computation, our results not only improve performance but also have the potential to enable quantum computation sooner than otherwise possible.