Small but Significant: On the Promise of Small Language Models for Accessible AIED

GPT has become nearly synonymous with large language models (LLMs), an increasingly popular term in AIED proceedings. A simple keyword-based search reveals that 61% of the 76 long and short papers presented at AIED 2024 describe novel solutions using LLMs to address some of the long-standing challenges in education, and 43% specifically mention GPT. Although LLMs pioneered by GPT create exciting opportunities to strengthen the impact of AI on education, we argue that the field's predominant focus on GPT and other resource-intensive LLMs (with more than 10B parameters) risks neglecting the potential impact that small language models (SLMs) can make in providing resource-constrained institutions with equitable and affordable access to high-quality AI tools. Supported by positive results on knowledge component (KC) discovery, a critical challenge in AIED, we demonstrate that SLMs such as Phi-2 can produce an effective solution without elaborate prompting strategies. Hence, we call for more attention to developing SLM-based AIED approaches.

KCluster: An LLM-based Clustering Approach to Knowledge Component Discovery

Educators evaluate student knowledge using knowledge component (KC) models that map assessment questions to KCs. Still, designing KC models for large question banks remains an insurmountable challenge for instructors who need to analyze each question by hand. The growing use of Generative AI in education is expected only to aggravate this chronic deficiency of expert-designed KC models, as course engineers designing KCs struggle to keep up with the pace at which questions are generated. In this work, we propose KCluster, a novel KC discovery algorithm based on identifying clusters of congruent questions according to a new similarity metric induced by a large language model (LLM). We demonstrate in three datasets that an LLM can create an effective metric of question similarity, which a clustering algorithm can use to create KC models from questions with minimal human effort. Combining the strengths of LLM and clustering, KCluster generates descriptive KC labels and discovers KC models that predict student performance better than the best expert-designed models available. In anticipation of future work, we illustrate how KCluster can reveal insights into difficult KCs and suggest improvements to instruction.

Low latency optical-based mode tracking with machine learning deployed on FPGAs on a tokamak

Active feedback control in magnetic confinement fusion devices is desirable to mitigate plasma instabilities and enable robust operation. Optical high-speed cameras provide a powerful, non-invasive diagnostic and can be suitable for these applications. In this study, we process fast camera data, at rates exceeding 100kfps, on $\textit{in situ}$ Field Programmable Gate Array (FPGA) hardware to track magnetohydrodynamic (MHD) mode evolution and generate control signals in real-time. Our system utilizes a convolutional neural network (CNN) model which predicts the $n$=1 MHD mode amplitude and phase using camera images with better accuracy than other tested non-deep-learning-based methods. By implementing this model directly within the standard FPGA readout hardware of the high-speed camera diagnostic, our mode tracking system achieves a total trigger-to-output latency of 17.6$\mu$s and a throughput of up to 120kfps. This study at the High Beta Tokamak-Extended Pulse (HBT-EP) experiment demonstrates an FPGA-based high-speed camera data acquisition and processing system, enabling application in real-time machine-learning-based tokamak diagnostic and control as well as potential applications in other scientific domains.

Sinusoidal Flow: A Fast Invertible Autoregressive Flow

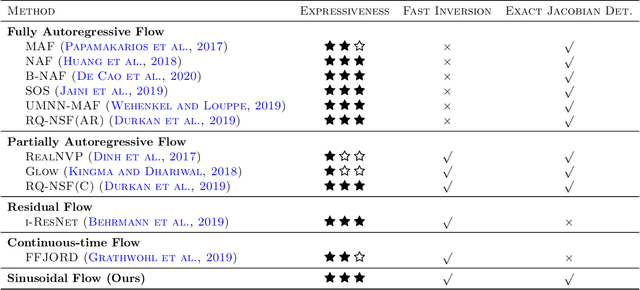
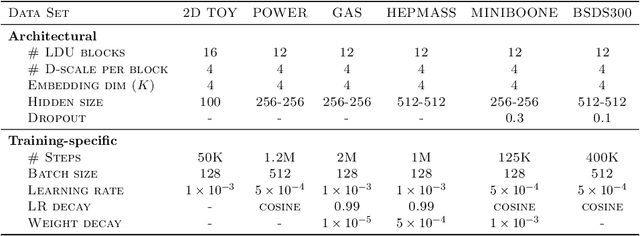
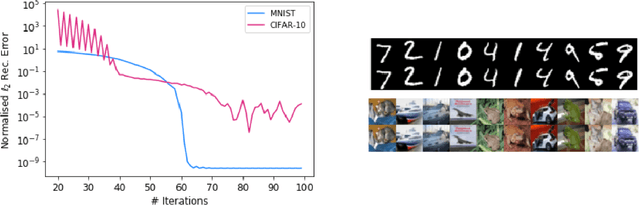
Normalising flows offer a flexible way of modelling continuous probability distributions. We consider expressiveness, fast inversion and exact Jacobian determinant as three desirable properties a normalising flow should possess. However, few flow models have been able to strike a good balance among all these properties. Realising that the integral of a convex sum of sinusoidal functions squared leads to a bijective residual transformation, we propose Sinusoidal Flow, a new type of normalising flows that inherits the expressive power and triangular Jacobian from fully autoregressive flows while guaranteed by Banach fixed-point theorem to remain fast invertible and thereby obviate the need for sequential inversion typically required in fully autoregressive flows. Experiments show that our Sinusoidal Flow is not only able to model complex distributions, but can also be reliably inverted to generate realistic-looking samples even with many layers of transformations stacked.