Semi-Supervised Endmember Identification In Nonlinear Spectral Mixtures Via Semantic Representation

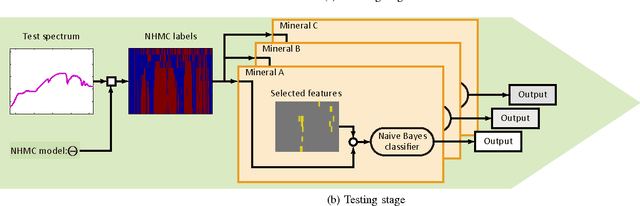
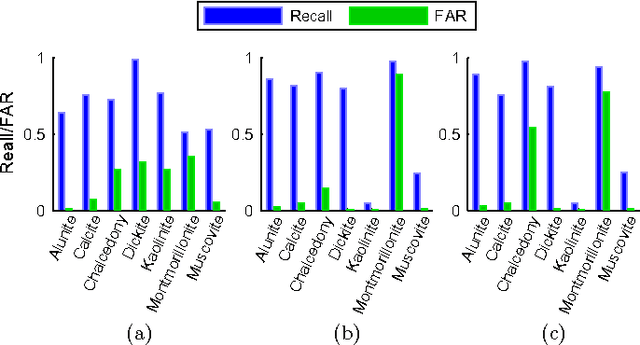
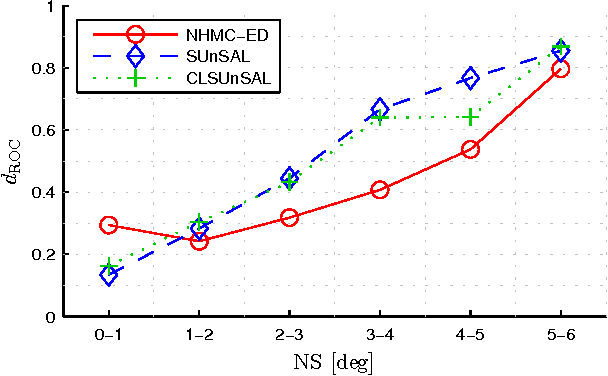
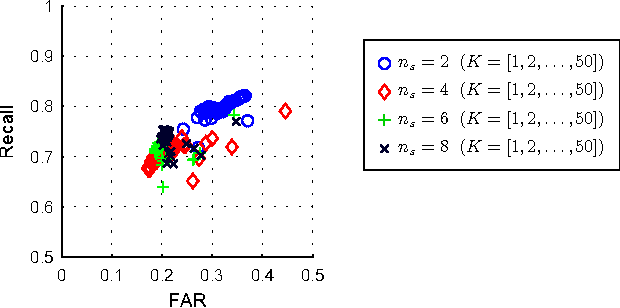
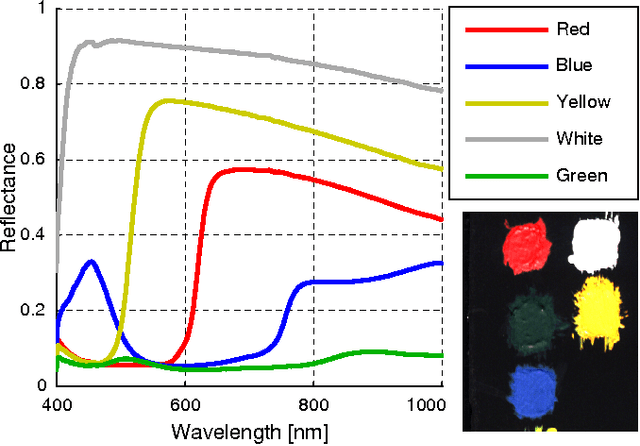
This paper proposes a new hyperspectral unmixing method for nonlinearly mixed hyperspectral data using a semantic representation in a semi-supervised fashion, assuming the availability of a spectral reference library. Existing semi-supervised unmixing algorithms select members from an endmember library that are present at each of the pixels; most such methods assume a linear mixing model. However, those methods will fail in the presence of nonlinear mixing among the observed spectra. To address this issue, we develop an endmember selection method using a recently proposed semantic spectral representation obtained via non-homogeneous hidden Markov chain (NHMC) model for a wavelet transform of the spectra. The semantic representation can encode spectrally discriminative features for any observed spectrum and, therefore, our proposed method can perform endmember selection without any assumption on the mixing model. Experimental results show that in the presence of sufficiently nonlinear mixing our proposed method outperforms dictionary-based sparse unmixing approaches based on linear models.

Perfect Recovery Conditions For Non-Negative Sparse Modeling

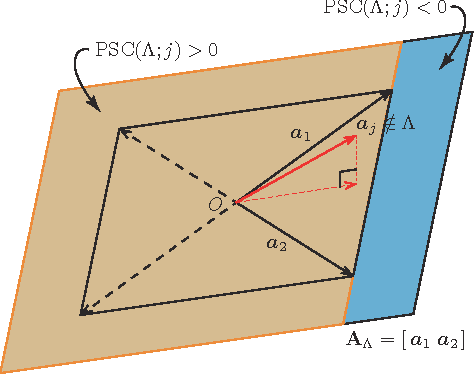
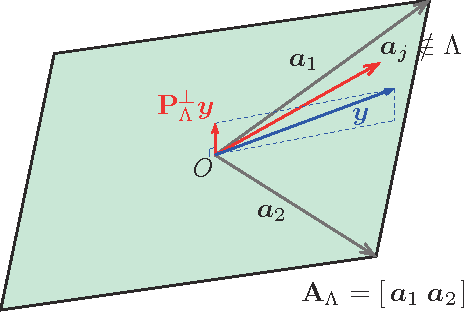
Sparse modeling has been widely and successfully used in many applications such as computer vision, machine learning, and pattern recognition. Accompanied with those applications, significant research has studied the theoretical limits and algorithm design for convex relaxations in sparse modeling. However, theoretical analyses on non-negative versions of sparse modeling are limited in the literature either to a noiseless setting or a scenario with a specific statistical noise model such as Gaussian noise. This paper studies the performance of non-negative sparse modeling in a more general scenario where the observed signals have an unknown arbitrary distortion, especially focusing on non-negativity constrained and L1-penalized least squares, and gives an exact bound for which this problem can recover the correct signal elements. We pose two conditions to guarantee the correct signal recovery: minimum coefficient condition (MCC) and nonlinearity vs. subset coherence condition (NSCC). The former defines the minimum weight for each of the correct atoms present in the signal and the latter defines the tolerable deviation from the linear model relative to the positive subset coherence (PSC), a novel type of "coherence" metric. We provide rigorous performance guarantees based on these conditions and experimentally verify their precise predictive power in a hyperspectral data unmixing application.

Wavelet-Based Semantic Features for Hyperspectral Signature Discrimination

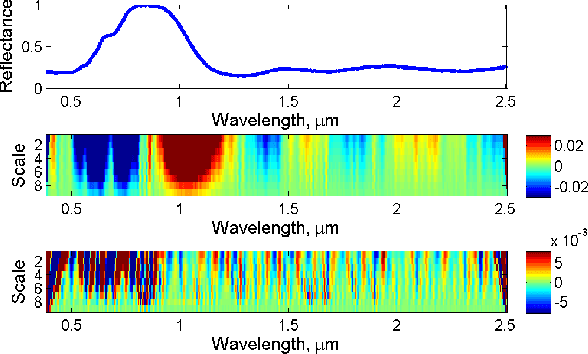
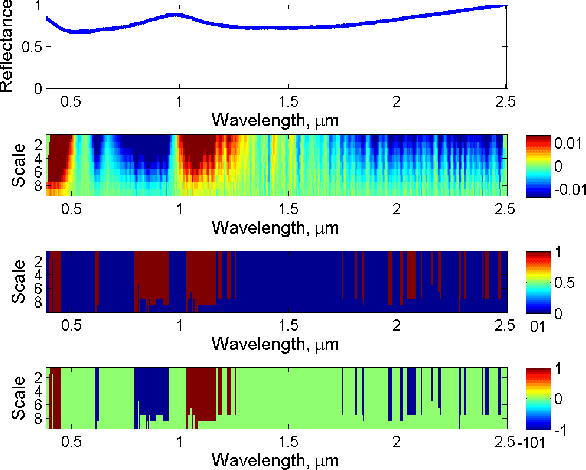
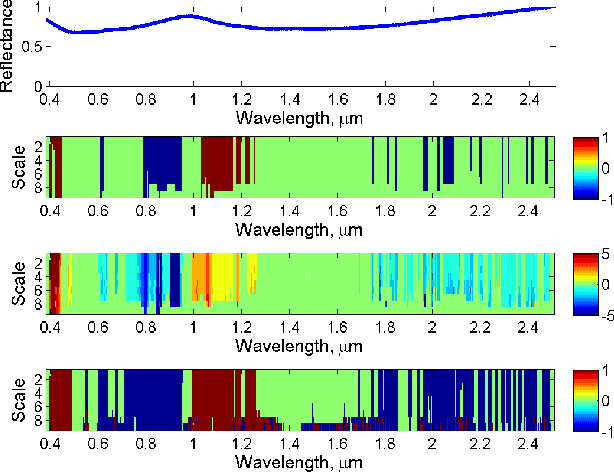
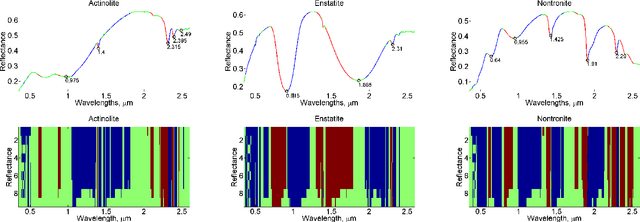
Hyperspectral signature classification is a quantitative analysis approach for hyperspectral imagery which performs detection and classification of the constituent materials at the pixel level in the scene. The classification procedure can be operated directly on hyperspectral data or performed by using some features extracted from the corresponding hyperspectral signatures containing information like the signature's energy or shape. In this paper, we describe a technique that applies non-homogeneous hidden Markov chain (NHMC) models to hyperspectral signature classification. The basic idea is to use statistical models (such as NHMC) to characterize wavelet coefficients which capture the spectrum semantics (i.e., structural information) at multiple levels. Experimental results show that the approach based on NHMC models can outperform existing approaches relevant in classification tasks.