Perfect Recovery Conditions For Non-Negative Sparse Modeling
Paper and Code
Sep 20, 2016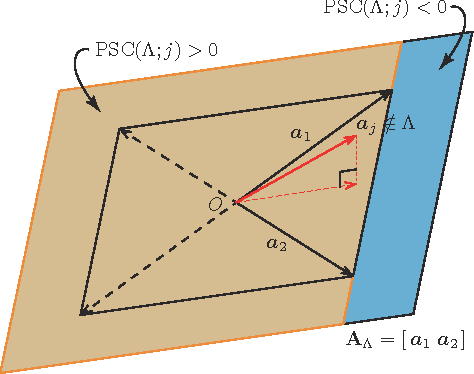
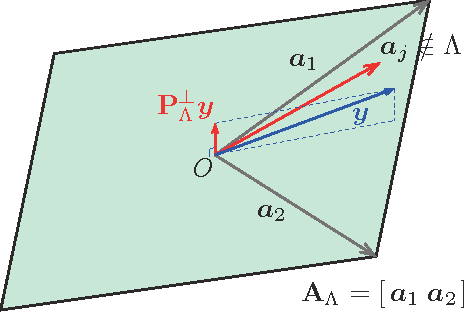

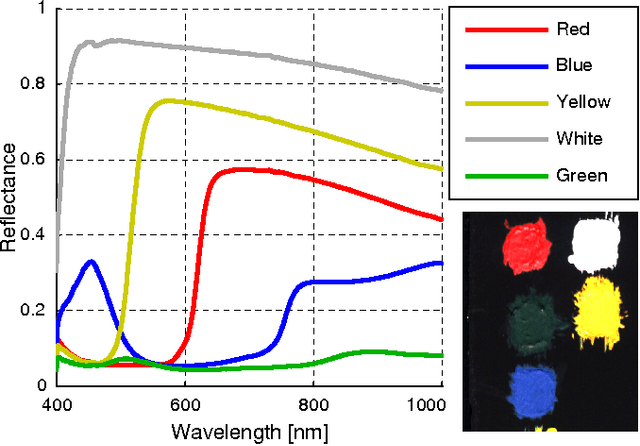
Sparse modeling has been widely and successfully used in many applications such as computer vision, machine learning, and pattern recognition. Accompanied with those applications, significant research has studied the theoretical limits and algorithm design for convex relaxations in sparse modeling. However, theoretical analyses on non-negative versions of sparse modeling are limited in the literature either to a noiseless setting or a scenario with a specific statistical noise model such as Gaussian noise. This paper studies the performance of non-negative sparse modeling in a more general scenario where the observed signals have an unknown arbitrary distortion, especially focusing on non-negativity constrained and L1-penalized least squares, and gives an exact bound for which this problem can recover the correct signal elements. We pose two conditions to guarantee the correct signal recovery: minimum coefficient condition (MCC) and nonlinearity vs. subset coherence condition (NSCC). The former defines the minimum weight for each of the correct atoms present in the signal and the latter defines the tolerable deviation from the linear model relative to the positive subset coherence (PSC), a novel type of "coherence" metric. We provide rigorous performance guarantees based on these conditions and experimentally verify their precise predictive power in a hyperspectral data unmixing application.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge