DC Algorithm for Estimation of Sparse Gaussian Graphical Models

Sparse estimation for Gaussian graphical models is a crucial technique for making the relationships among numerous observed variables more interpretable and quantifiable. Various methods have been proposed, including graphical lasso, which utilizes the $\ell_1$ norm as a regularization term, as well as methods employing non-convex regularization terms. However, most of these methods approximate the $\ell_0$ norm with convex functions. To estimate more accurate solutions, it is desirable to treat the $\ell_0$ norm directly as a regularization term. In this study, we formulate the sparse estimation problem for Gaussian graphical models using the $\ell_0$ norm and propose a method to solve this problem using the Difference of Convex functions Algorithm (DCA). Specifically, we convert the $\ell_0$ norm constraint into an equivalent largest-$K$ norm constraint, reformulate the constrained problem into a penalized form, and solve it using the DC algorithm (DCA). Furthermore, we designed an algorithm that efficiently computes using graphical lasso. Experimental results with synthetic data show that our method yields results that are equivalent to or better than existing methods. Comparisons of model learning through cross-validation confirm that our method is particularly advantageous in selecting true edges.

Robust personalized pricing under uncertainty of purchase probabilities

This paper is concerned with personalized pricing models aimed at maximizing the expected revenues or profits for a single item. While it is essential for personalized pricing to predict the purchase probabilities for each consumer, these predicted values are inherently subject to unavoidable errors that can negatively impact the realized revenues and profits. To address this issue, we focus on robust optimization techniques that yield reliable solutions to optimization problems under uncertainty. Specifically, we propose a robust optimization model for personalized pricing that accounts for the uncertainty of predicted purchase probabilities. This model can be formulated as a mixed-integer linear optimization problem, which can be solved exactly using mathematical optimization solvers. We also develop a Lagrangian decomposition algorithm combined with line search to efficiently find high-quality solutions for large-scale optimization problems. Experimental results demonstrate the effectiveness of our robust optimization model and highlight the utility of our Lagrangian decomposition algorithm in terms of both computational efficiency and solution quality.

Strategic Coupon Allocation for Increasing Providers' Sales Experiences in Two-sided Marketplaces

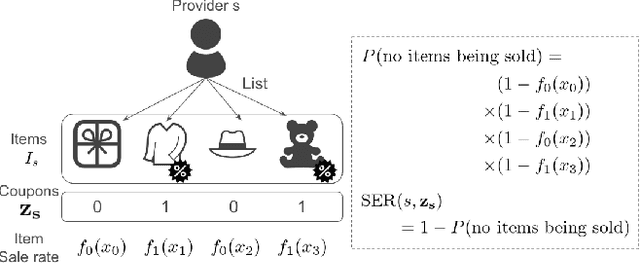
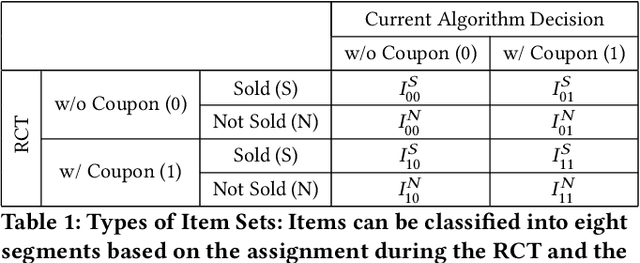
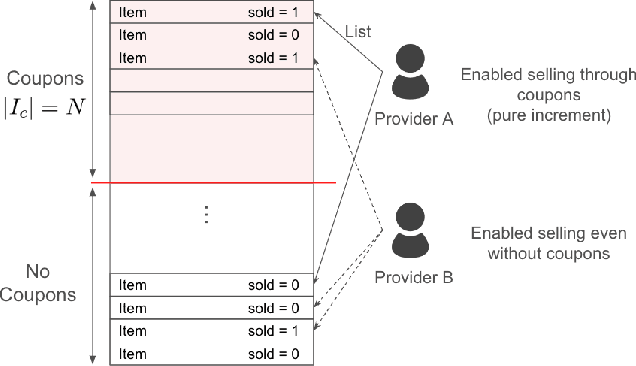
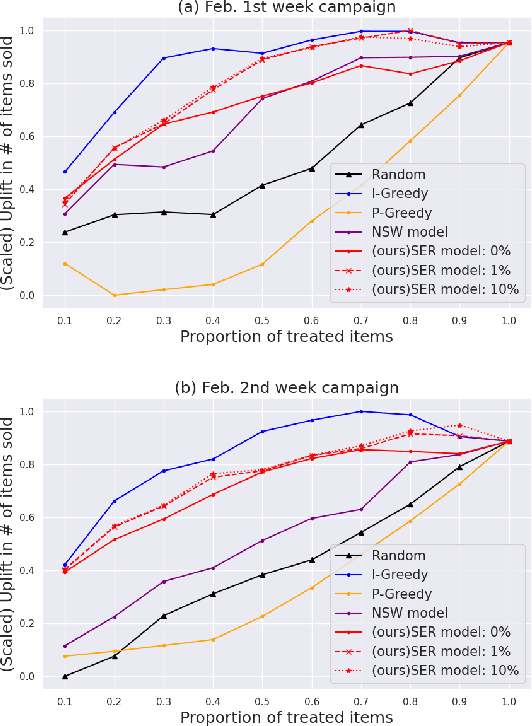
In a two-sided marketplace, network effects are crucial for competitiveness, and platforms need to retain users through advanced customer relationship management as much as possible. Maintaining numerous providers' stable and active presence on the platform is highly important to enhance the marketplace's scale and diversity. The strongest motivation for providers to continue using the platform is to realize actual profits through sales. Then, we propose a personalized promotion to increase the number of successful providers with sales experiences on the platform. The main contributions of our research are twofold. First, we introduce a new perspective in provider management with the distribution of successful sales experiences. Second, we propose a personalized promotion optimization method to maximize the number of providers' sales experiences. By utilizing this approach, we ensure equal opportunities for providers to experience sales without being monopolized by a few providers. Through experiments using actual data on coupon distribution, we confirm that our method enables the implementation of coupon allocation strategies that significantly increase the total number of providers having sales experiences.

Fast solution to the fair ranking problem using the Sinkhorn algorithm

In two-sided marketplaces such as online flea markets, recommender systems for providing consumers with personalized item rankings play a key role in promoting transactions between providers and consumers. Meanwhile, two-sided marketplaces face the problem of balancing consumer satisfaction and fairness among items to stimulate activity of item providers. Saito and Joachims (2022) devised an impact-based fair ranking method for maximizing the Nash social welfare based on fair division; however, this method, which requires solving a large-scale constrained nonlinear optimization problem, is very difficult to apply to practical-scale recommender systems. We thus propose a fast solution to the impact-based fair ranking problem. We first transform the fair ranking problem into an unconstrained optimization problem and then design a gradient ascent method that repeatedly executes the Sinkhorn algorithm. Experimental results demonstrate that our algorithm provides fair rankings of high quality and is about 1000 times faster than application of commercial optimization software.

Robust portfolio optimization for recommender systems considering uncertainty of estimated statistics

This paper is concerned with portfolio optimization models for creating high-quality lists of recommended items to balance the accuracy and diversity of recommendations. However, the statistics (i.e., expectation and covariance of ratings) required for mean--variance portfolio optimization are subject to inevitable estimation errors. To remedy this situation, we focus on robust optimization techniques that derive reliable solutions to uncertain optimization problems. Specifically, we propose a robust portfolio optimization model that copes with the uncertainty of estimated statistics based on the cardinality-based uncertainty sets. This robust portfolio optimization model can be reduced to a mixed-integer linear optimization problem, which can be solved exactly using mathematical optimization solvers. Experimental results using two publicly available rating datasets demonstrate that our method can improve not only the recommendation accuracy but also the diversity of recommendations compared with conventional mean--variance portfolio optimization models. Notably, our method has the potential to improve the recommendation quality of various rating prediction algorithms.

Container pre-marshalling problem minimizing CV@R under uncertainty of ship arrival times

This paper is concerned with the container pre-marshalling problem, which involves relocating containers in the storage area so that they can be efficiently loaded onto ships without reshuffles. In reality, however, ship arrival times are affected by various external factors, which can cause the order of container retrieval to be different from the initial plan. To represent such uncertainty, we generate multiple scenarios from a multivariate probability distribution of ship arrival times. We derive a mixed-integer linear optimization model to find an optimal container layout such that the conditional value-at-risk is minimized for the number of misplaced containers responsible for reshuffles. Moreover, we devise an exact algorithm based on the cutting-plane method to handle large-scale problems. Numerical experiments using synthetic datasets demonstrate that our method can produce high-quality container layouts compared with the conventional robust optimization model. Additionally, our algorithm can speed up the computation of solving large-scale problems.

Privacy-preserving recommender system using the data collaboration analysis for distributed datasets

In order to provide high-quality recommendations for users, it is desirable to share and integrate multiple datasets held by different parties. However, when sharing such distributed datasets, we need to protect personal and confidential information contained in the datasets. To this end, we establish a framework for privacy-preserving recommender systems using the data collaboration analysis of distributed datasets. Numerical experiments with two public rating datasets demonstrate that our privacy-preserving method for rating prediction can improve the prediction accuracy for distributed datasets. This study opens up new possibilities for privacy-preserving techniques in recommender systems.

Robust portfolio optimization model for electronic coupon allocation

Currently, many e-commerce websites issue online/electronic coupons as an effective tool for promoting sales of various products and services. We focus on the problem of optimally allocating coupons to customers subject to a budget constraint on an e-commerce website. We apply a robust portfolio optimization model based on customer segmentation to the coupon allocation problem. We also validate the efficacy of our method through numerical experiments using actual data from randomly distributed coupons. Main contributions of our research are twofold. First, we handle six types of coupons, thereby making it extremely difficult to accurately estimate the difference in the effects of various coupons. Second, we demonstrate from detailed numerical results that the robust optimization model achieved larger uplifts of sales than did the commonly-used multiple-choice knapsack model and the conventional mean-variance optimization model. Our results open up great potential for robust portfolio optimization as an effective tool for practical coupon allocation.

New Solutions Based on the Generalized Eigenvalue Problem for the Data Collaboration Analysis

In recent years, the accumulation of data across various institutions has garnered attention for the technology of confidential data analysis, which improves analytical accuracy by sharing data between multiple institutions while protecting sensitive information. Among these methods, Data Collaboration Analysis (DCA) is noted for its efficiency in terms of computational cost and communication load, facilitating data sharing and analysis across different institutions while safeguarding confidential information. However, existing optimization problems for determining the necessary collaborative functions have faced challenges, such as the optimal solution for the collaborative representation often being a zero matrix and the difficulty in understanding the process of deriving solutions. This research addresses these issues by formulating the optimization problem through the segmentation of matrices into column vectors and proposing a solution method based on the generalized eigenvalue problem. Additionally, we demonstrate methods for constructing collaborative functions more effectively through weighting and the selection of efficient algorithms suited to specific situations. Experiments using real-world datasets have shown that our proposed formulation and solution for the collaborative function optimization problem achieve superior predictive accuracy compared to existing methods.

Feature subset selection for kernel SVM classification via mixed-integer optimization

We study the mixed-integer optimization (MIO) approach to feature subset selection in nonlinear kernel support vector machines (SVMs) for binary classification. First proposed for linear regression in the 1970s, this approach has recently moved into the spotlight with advances in optimization algorithms and computer hardware. The goal of this paper is to establish an MIO approach for selecting the best subset of features for kernel SVM classification. To measure the performance of subset selection, we use the kernel-target alignment, which is the distance between the centroids of two response classes in a high-dimensional feature space. We propose a mixed-integer linear optimization (MILO) formulation based on the kernel-target alignment for feature subset selection, and this MILO problem can be solved to optimality using optimization software. We also derive a reduced version of the MILO problem to accelerate our MILO computations. Experimental results show good computational efficiency for our MILO formulation with the reduced problem. Moreover, our method can often outperform the linear-SVM-based MILO formulation and recursive feature elimination in prediction performance, especially when there are relatively few data instances.