Yubin Park
PaloBoost: An Overfitting-robust TreeBoost with Out-of-Bag Sample Regularization Techniques
Jul 22, 2018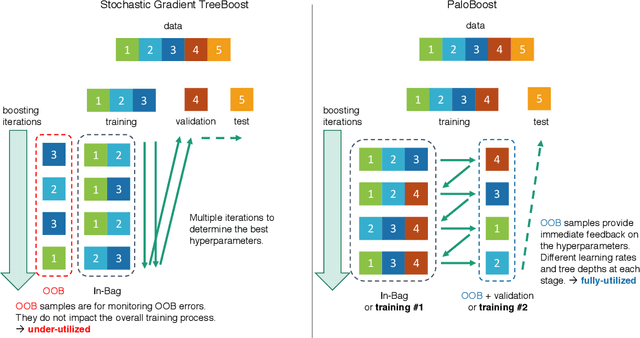
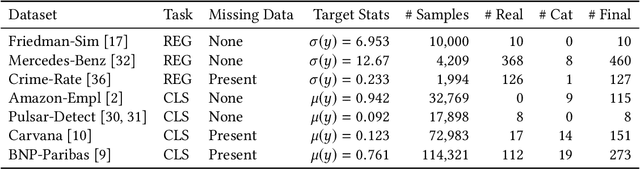

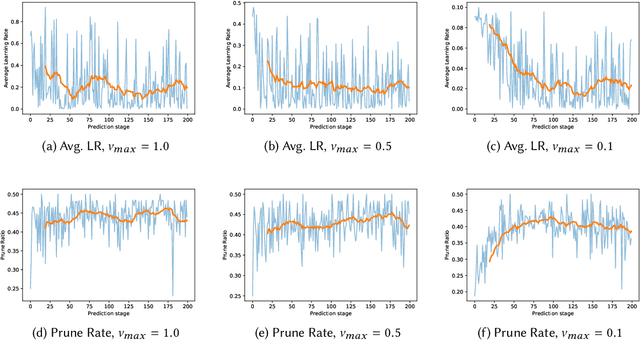
Abstract:Stochastic Gradient TreeBoost is often found in many winning solutions in public data science challenges. Unfortunately, the best performance requires extensive parameter tuning and can be prone to overfitting. We propose PaloBoost, a Stochastic Gradient TreeBoost model that uses novel regularization techniques to guard against overfitting and is robust to parameter settings. PaloBoost uses the under-utilized out-of-bag samples to perform gradient-aware pruning and estimate adaptive learning rates. Unlike other Stochastic Gradient TreeBoost models that use the out-of-bag samples to estimate test errors, PaloBoost treats the samples as a second batch of training samples to prune the trees and adjust the learning rates. As a result, PaloBoost can dynamically adjust tree depths and learning rates to achieve faster learning at the start and slower learning as the algorithm converges. We illustrate how these regularization techniques can be efficiently implemented and propose a new formula for calculating feature importance to reflect the node coverages and learning rates. Extensive experimental results on seven datasets demonstrate that PaloBoost is robust to overfitting, is less sensitivity to the parameters, and can also effectively identify meaningful features.
ACDC: $α$-Carving Decision Chain for Risk Stratification
Jun 16, 2016

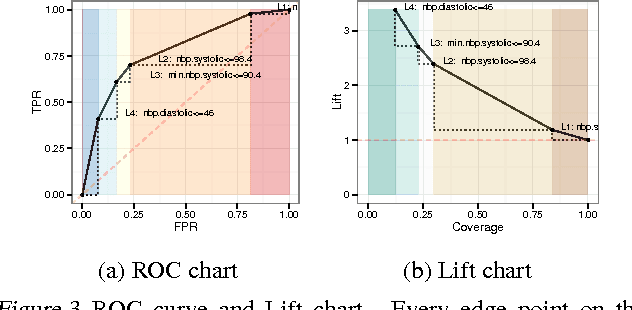

Abstract:In many healthcare settings, intuitive decision rules for risk stratification can help effective hospital resource allocation. This paper introduces a novel variant of decision tree algorithms that produces a chain of decisions, not a general tree. Our algorithm, $\alpha$-Carving Decision Chain (ACDC), sequentially carves out "pure" subsets of the majority class examples. The resulting chain of decision rules yields a pure subset of the minority class examples. Our approach is particularly effective in exploring large and class-imbalanced health datasets. Moreover, ACDC provides an interactive interpretation in conjunction with visual performance metrics such as Receiver Operating Characteristics curve and Lift chart.
Perturbed Gibbs Samplers for Synthetic Data Release
Dec 18, 2013
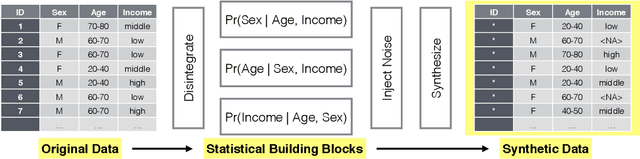


Abstract:We propose a categorical data synthesizer with a quantifiable disclosure risk. Our algorithm, named Perturbed Gibbs Sampler, can handle high-dimensional categorical data that are often intractable to represent as contingency tables. The algorithm extends a multiple imputation strategy for fully synthetic data by utilizing feature hashing and non-parametric distribution approximations. California Patient Discharge data are used to demonstrate statistical properties of the proposed synthesizing methodology. Marginal and conditional distributions, as well as the coefficients of regression models built on the synthesized data are compared to those obtained from the original data. Intruder scenarios are simulated to evaluate disclosure risks of the synthesized data from multiple angles. Limitations and extensions of the proposed algorithm are also discussed.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge