Yuanyi Liu
A Dynamic-Neighbor Particle Swarm Optimizer for Accurate Latent Factor Analysis
Feb 23, 2023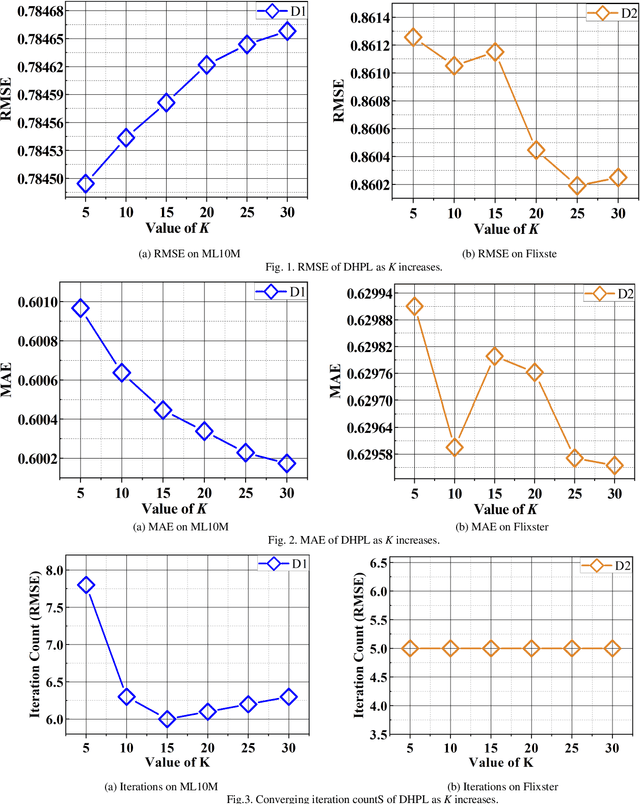
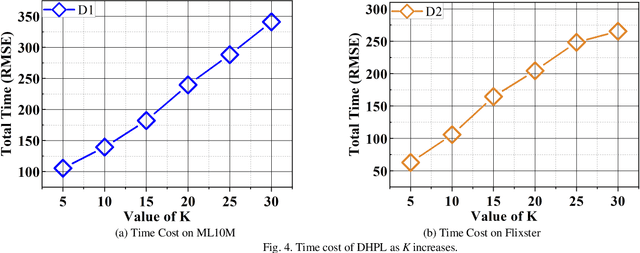

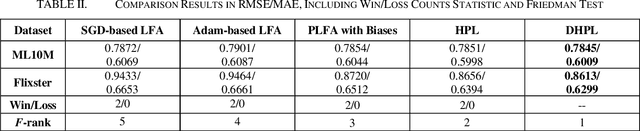
Abstract:High-Dimensional and Incomplete matrices, which usually contain a large amount of valuable latent information, can be well represented by a Latent Factor Analysis model. The performance of an LFA model heavily rely on its optimization process. Thereby, some prior studies employ the Particle Swarm Optimization to enhance an LFA model's optimization process. However, the particles within the swarm follow the static evolution paths and only share the global best information, which limits the particles' searching area to cause sub-optimum issue. To address this issue, this paper proposes a Dynamic-neighbor-cooperated Hierarchical PSO-enhanced LFA model with two-fold main ideas. First is the neighbor-cooperated strategy, which enhances the randomly chosen neighbor's velocity for particles' evolution. Second is the dynamic hyper-parameter tunning. Extensive experiments on two benchmark datasets are conducted to evaluate the proposed DHPL model. The results substantiate that DHPL achieves a higher accuracy without hyper-parameters tunning than the existing PSO-incorporated LFA models in representing an HDI matrix.
An Adam-enhanced Particle Swarm Optimizer for Latent Factor Analysis
Feb 23, 2023Abstract:Digging out the latent information from large-scale incomplete matrices is a key issue with challenges. The Latent Factor Analysis (LFA) model has been investigated in depth to an alyze the latent information. Recently, Swarm Intelligence-related LFA models have been proposed and adopted widely to improve the optimization process of LFA with high efficiency, i.e., the Particle Swarm Optimization (PSO)-LFA model. However, the hyper-parameters of the PSO-LFA model have to tune manually, which is inconvenient for widely adoption and limits the learning rate as a fixed value. To address this issue, we propose an Adam-enhanced Hierarchical PSO-LFA model, which refines the latent factors with a sequential Adam-adjusting hyper-parameters PSO algorithm. First, we design the Adam incremental vector for a particle and construct the Adam-enhanced evolution process for particles. Second, we refine all the latent factors of the target matrix sequentially with our proposed Adam-enhanced PSO's process. The experimental results on four real datasets demonstrate that our proposed model achieves higher prediction accuracy with its peers.
An Adam-adjusting-antennae BAS Algorithm for Refining Latent Factors
Aug 13, 2022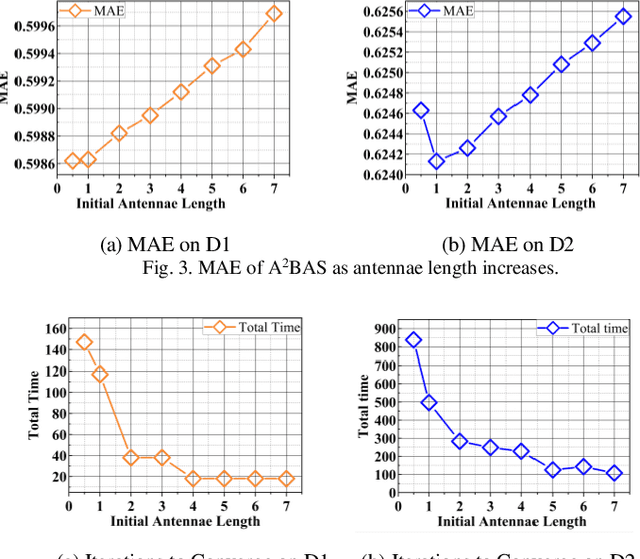

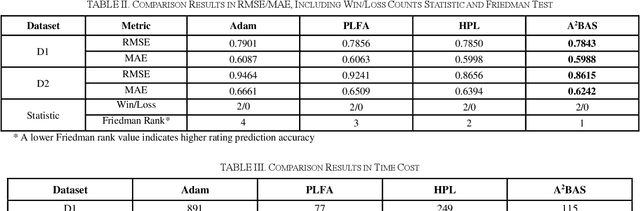
Abstract:Extracting the latent information in high-dimensional and incomplete matrices is an important and challenging issue. The Latent Factor Analysis (LFA) model can well handle the high-dimensional matrices analysis. Recently, Particle Swarm Optimization (PSO)-incorporated LFA models have been proposed to tune the hyper-parameters adaptively with high efficiency. However, the incorporation of PSO causes the premature problem. To address this issue, we propose a sequential Adam-adjusting-antennae BAS (A2BAS) optimization algorithm, which refines the latent factors obtained by the PSO-incorporated LFA model. The A2BAS algorithm consists of two sub-algorithms. First, we design an improved BAS algorithm which adjusts beetles' antennae and step-size with Adam; Second, we implement the improved BAS algorithm to optimize all the row and column latent factors sequentially. With experimental results on two real high-dimensional matrices, we demonstrate that our algorithm can effectively solve the premature convergence issue.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge