Deep polytopic autoencoders for low-dimensional linear parameter-varying approximations and nonlinear feedback design

Polytopic autoencoders provide low-dimensional parametrizations of states in a polytope. For nonlinear PDEs, this is readily applied to low-dimensional linear parameter-varying (LPV) approximations as they have been exploited for efficient nonlinear controller design via series expansions of the solution to the state-dependent Riccati equation. In this work, we develop a polytopic autoencoder for control applications and show how it outperforms standard linear approaches in view of LPV approximations of nonlinear systems and how the particular architecture enables higher order series expansions at little extra computational effort. We illustrate the properties and potentials of this approach to computational nonlinear controller design for large-scale systems with a thorough numerical study.

Polytopic Autoencoders with Smooth Clustering for Reduced-order Modelling of Flows

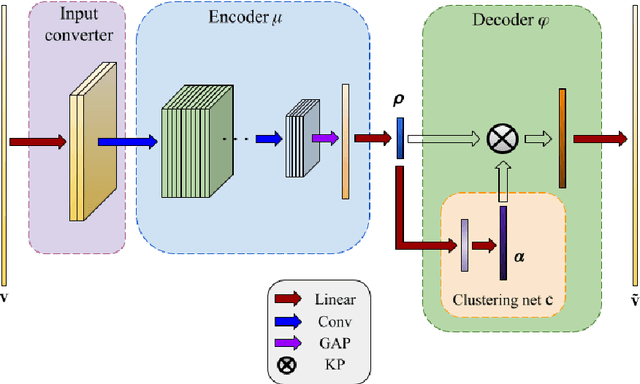
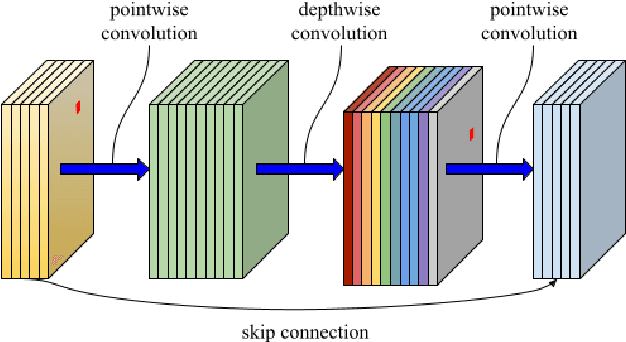
With the advancement of neural networks, there has been a notable increase, both in terms of quantity and variety, in research publications concerning the application of autoencoders to reduced-order models. We propose a polytopic autoencoder architecture that includes a lightweight nonlinear encoder, a convex combination decoder, and a smooth clustering network. Supported by several proofs, the model architecture ensures that all reconstructed states lie within a polytope, accompanied by a metric indicating the quality of the constructed polytopes, referred to as polytope error. Additionally, it offers a minimal number of convex coordinates for polytopic linear-parameter varying systems while achieving acceptable reconstruction errors compared to proper orthogonal decomposition (POD). To validate our proposed model, we conduct simulations involving two flow scenarios with the incompressible Navier-Stokes equation. Numerical results demonstrate the guaranteed properties of the model, low reconstruction errors compared to POD, and the improvement in error using a clustering network.

Going Deeper with Five-point Stencil Convolutions for Reaction-Diffusion Equations

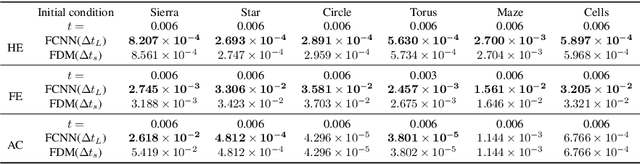
Physics-informed neural networks have been widely applied to partial differential equations with great success because the physics-informed loss essentially requires no observations or discretization. However, it is difficult to optimize model parameters, and these parameters must be trained for each distinct initial condition. To overcome these challenges in second-order reaction-diffusion type equations, a possible way is to use five-point stencil convolutional neural networks (FCNNs). FCNNs are trained using two consecutive snapshots, where the time step corresponds to the step size of the given snapshots. Thus, the time evolution of FCNNs depends on the time step, and the time step must satisfy its CFL condition to avoid blow-up solutions. In this work, we propose deep FCNNs that have large receptive fields to predict time evolutions with a time step larger than the threshold of the CFL condition. To evaluate our models, we consider the heat, Fisher's, and Allen-Cahn equations with diverse initial conditions. We demonstrate that deep FCNNs retain certain accuracies, in contrast to FDMs that blow up.

Convolutional Autoencoders, Clustering and POD for Low-dimensional Parametrization of Navier-Stokes Equations

Simulations of large-scale dynamical systems require expensive computations. Low-dimensional parametrization of high-dimensional states such as Proper Orthogonal Decomposition (POD) can be a solution to lessen the burdens by providing a certain compromise between accuracy and model complexity. However, for really low-dimensional parametrizations (for example for controller design) linear methods like the POD come to their natural limits so that nonlinear approaches will be the methods of choice. In this work we propose a convolutional autoencoder (CAE) consisting of a nonlinear encoder and an affine linear decoder and consider combinations with k-means clustering for improved encoding performance. The proposed set of methods is compared to the standard POD approach in two cylinder-wake scenarios modeled by the incompressible Navier-Stokes equations.

FCNN: Five-point stencil CNN for solving reaction-diffusion equations

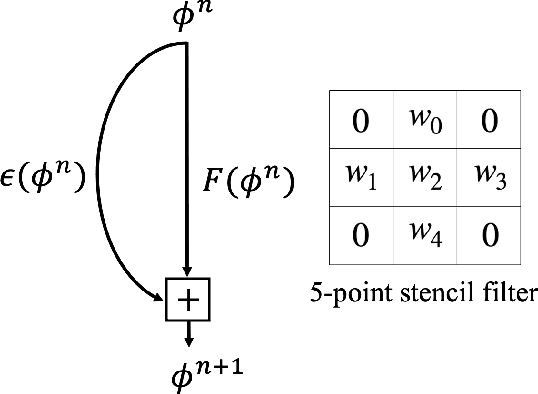
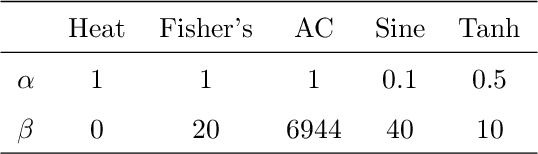
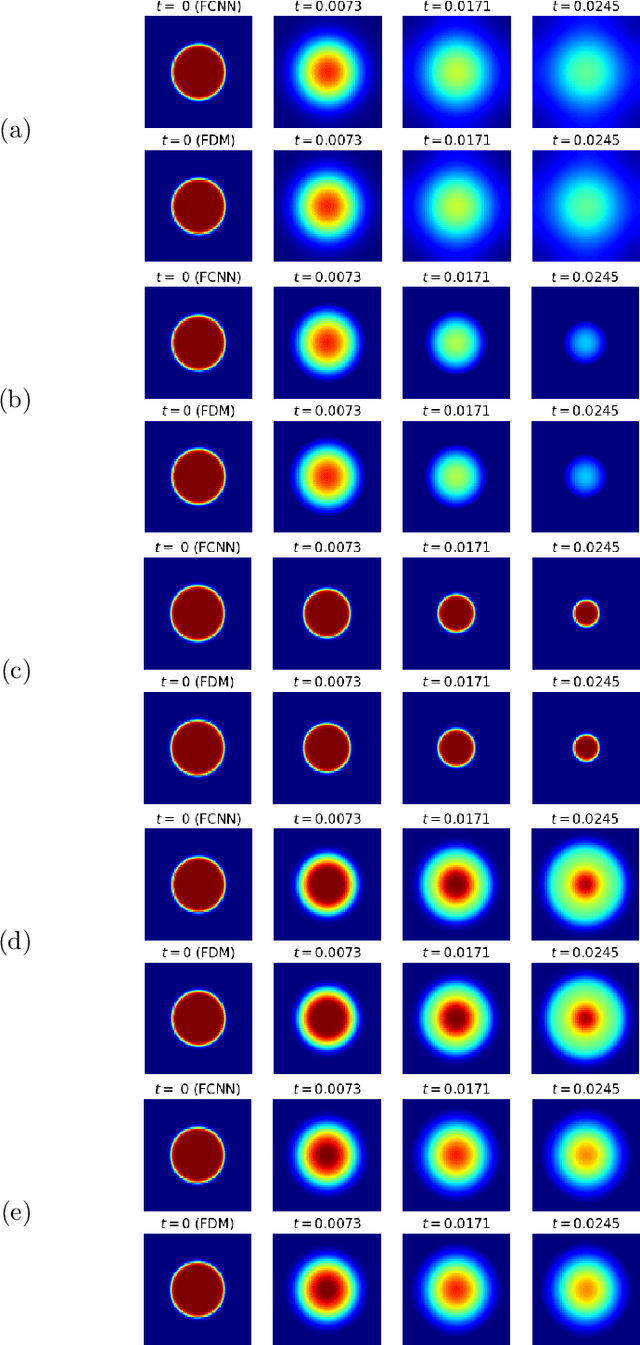
In this paper, we propose Five-point stencil CNN (FCNN) containing a five-point stencil kernel and a trainable approximation function. We consider reaction-diffusion type equations including heat, Fisher's, Allen-Cahn equations, and reaction-diffusion equations with trigonometric functions. Our proposed FCNN is trained well using few data and then can predict reaction-diffusion evolutions with unseen initial conditions. Also, our FCNN is trained well in the case of using noisy train data. We present various simulation results to demonstrate that our proposed FCNN is working well.

Disturbing Target Values for Neural Network Regularization

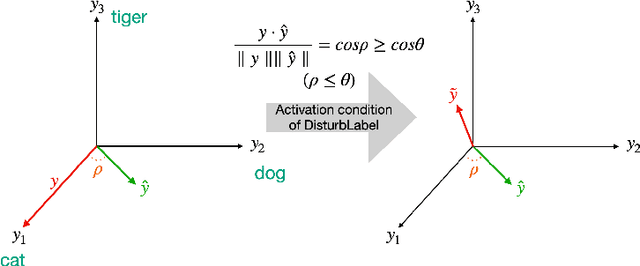
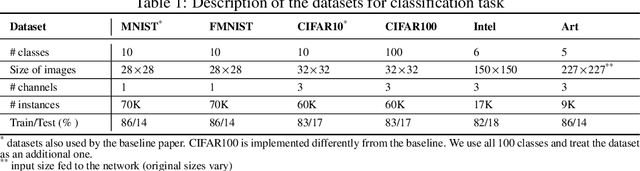
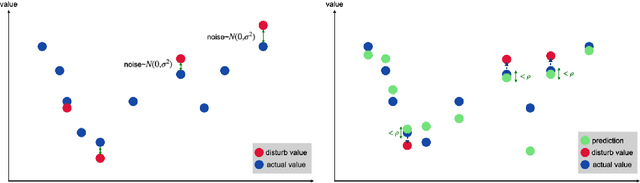
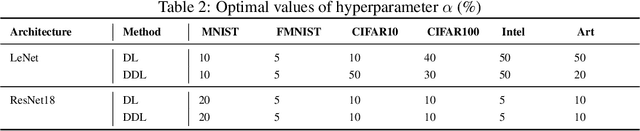
Diverse regularization techniques have been developed such as L2 regularization, Dropout, DisturbLabel (DL) to prevent overfitting. DL, a newcomer on the scene, regularizes the loss layer by flipping a small share of the target labels at random and training the neural network on this distorted data so as to not learn the training data. It is observed that high confidence labels during training cause the overfitting problem and DL selects disturb labels at random regardless of the confidence of labels. To solve this shortcoming of DL, we propose Directional DisturbLabel (DDL) a novel regularization technique that makes use of the class probabilities to infer the confident labels and using these labels to regularize the model. This active regularization makes use of the model behavior during training to regularize it in a more directed manner. To address regression problems, we also propose DisturbValue (DV), and DisturbError (DE). DE uses only predefined confident labels to disturb target values. DV injects noise into a portion of target values at random similar to DL. In this paper, 6 and 8 datasets are used to validate the robustness of our methods in classification and regression tasks respectively. Finally, we demonstrate that our methods are either comparable to or outperform DisturbLabel, L2 regularization, and Dropout. Also, we achieve the best performance in more than half the datasets by combining our methods with either L2 regularization or Dropout.