Going Deeper with Five-point Stencil Convolutions for Reaction-Diffusion Equations

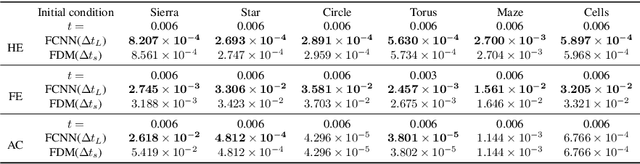
Physics-informed neural networks have been widely applied to partial differential equations with great success because the physics-informed loss essentially requires no observations or discretization. However, it is difficult to optimize model parameters, and these parameters must be trained for each distinct initial condition. To overcome these challenges in second-order reaction-diffusion type equations, a possible way is to use five-point stencil convolutional neural networks (FCNNs). FCNNs are trained using two consecutive snapshots, where the time step corresponds to the step size of the given snapshots. Thus, the time evolution of FCNNs depends on the time step, and the time step must satisfy its CFL condition to avoid blow-up solutions. In this work, we propose deep FCNNs that have large receptive fields to predict time evolutions with a time step larger than the threshold of the CFL condition. To evaluate our models, we consider the heat, Fisher's, and Allen-Cahn equations with diverse initial conditions. We demonstrate that deep FCNNs retain certain accuracies, in contrast to FDMs that blow up.

FCNN: Five-point stencil CNN for solving reaction-diffusion equations

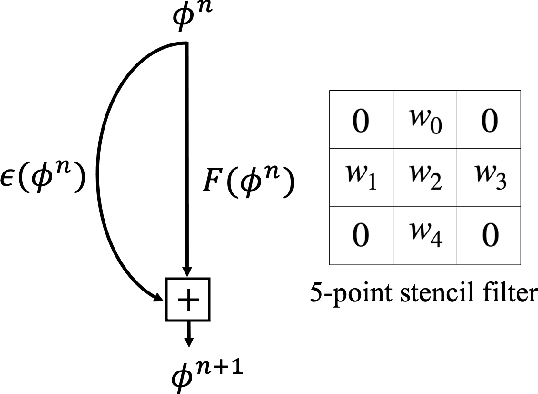
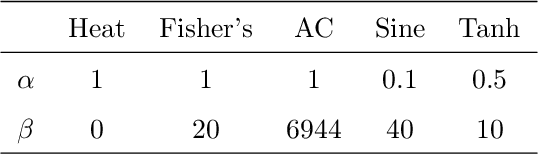
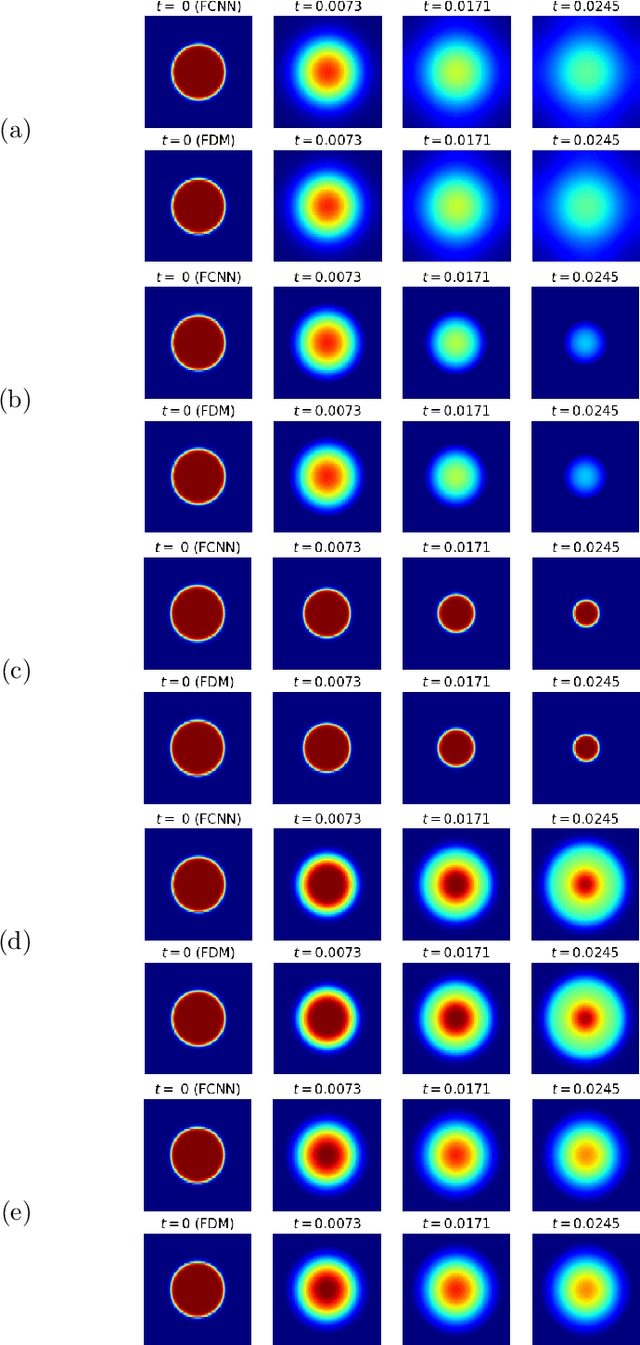
In this paper, we propose Five-point stencil CNN (FCNN) containing a five-point stencil kernel and a trainable approximation function. We consider reaction-diffusion type equations including heat, Fisher's, Allen-Cahn equations, and reaction-diffusion equations with trigonometric functions. Our proposed FCNN is trained well using few data and then can predict reaction-diffusion evolutions with unseen initial conditions. Also, our FCNN is trained well in the case of using noisy train data. We present various simulation results to demonstrate that our proposed FCNN is working well.