Deep polytopic autoencoders for low-dimensional linear parameter-varying approximations and nonlinear feedback design

Polytopic autoencoders provide low-dimensional parametrizations of states in a polytope. For nonlinear PDEs, this is readily applied to low-dimensional linear parameter-varying (LPV) approximations as they have been exploited for efficient nonlinear controller design via series expansions of the solution to the state-dependent Riccati equation. In this work, we develop a polytopic autoencoder for control applications and show how it outperforms standard linear approaches in view of LPV approximations of nonlinear systems and how the particular architecture enables higher order series expansions at little extra computational effort. We illustrate the properties and potentials of this approach to computational nonlinear controller design for large-scale systems with a thorough numerical study.

Polytopic Autoencoders with Smooth Clustering for Reduced-order Modelling of Flows

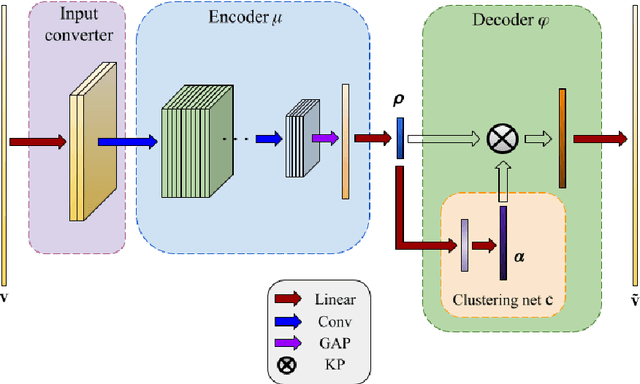
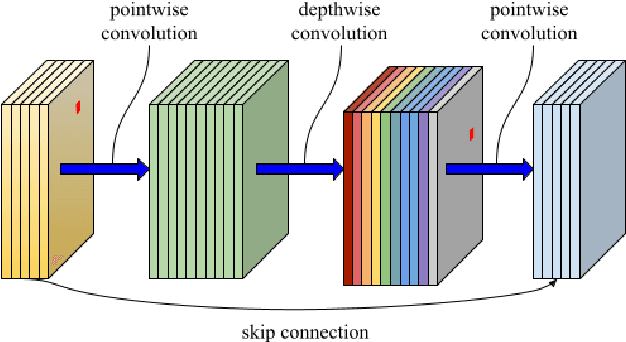
With the advancement of neural networks, there has been a notable increase, both in terms of quantity and variety, in research publications concerning the application of autoencoders to reduced-order models. We propose a polytopic autoencoder architecture that includes a lightweight nonlinear encoder, a convex combination decoder, and a smooth clustering network. Supported by several proofs, the model architecture ensures that all reconstructed states lie within a polytope, accompanied by a metric indicating the quality of the constructed polytopes, referred to as polytope error. Additionally, it offers a minimal number of convex coordinates for polytopic linear-parameter varying systems while achieving acceptable reconstruction errors compared to proper orthogonal decomposition (POD). To validate our proposed model, we conduct simulations involving two flow scenarios with the incompressible Navier-Stokes equation. Numerical results demonstrate the guaranteed properties of the model, low reconstruction errors compared to POD, and the improvement in error using a clustering network.

Convolutional Autoencoders, Clustering and POD for Low-dimensional Parametrization of Navier-Stokes Equations

Simulations of large-scale dynamical systems require expensive computations. Low-dimensional parametrization of high-dimensional states such as Proper Orthogonal Decomposition (POD) can be a solution to lessen the burdens by providing a certain compromise between accuracy and model complexity. However, for really low-dimensional parametrizations (for example for controller design) linear methods like the POD come to their natural limits so that nonlinear approaches will be the methods of choice. In this work we propose a convolutional autoencoder (CAE) consisting of a nonlinear encoder and an affine linear decoder and consider combinations with k-means clustering for improved encoding performance. The proposed set of methods is compared to the standard POD approach in two cylinder-wake scenarios modeled by the incompressible Navier-Stokes equations.

Operator Inference and Physics-Informed Learning of Low-Dimensional Models for Incompressible Flows

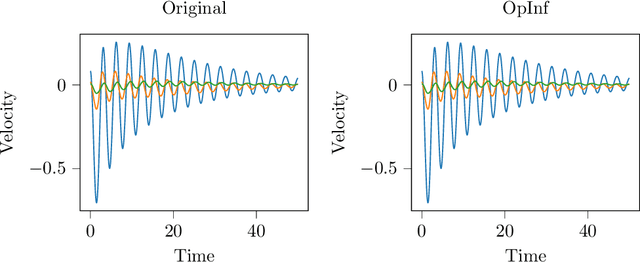
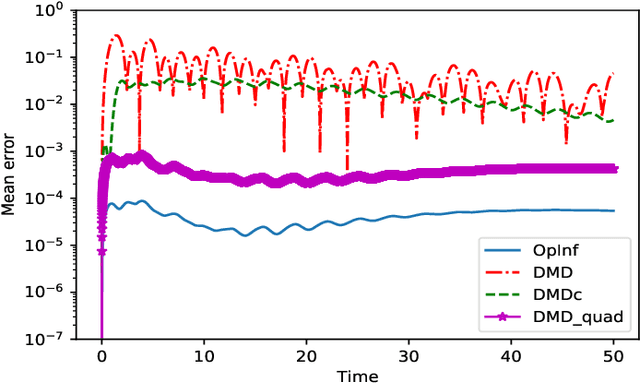
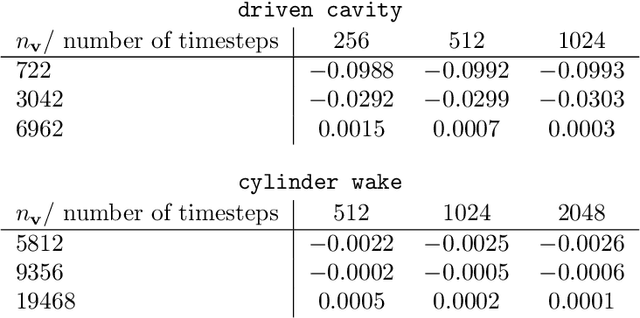
Reduced-order modeling has a long tradition in computational fluid dynamics. The ever-increasing significance of data for the synthesis of low-order models is well reflected in the recent successes of data-driven approaches such as Dynamic Mode Decomposition and Operator Inference. With this work, we suggest a new approach to learning structured low-order models for incompressible flow from data that can be used for engineering studies such as control, optimization, and simulation. To that end, we utilize the intrinsic structure of the Navier-Stokes equations for incompressible flows and show that learning dynamics of the velocity and pressure can be decoupled, thus leading to an efficient operator inference approach for learning the underlying dynamics of incompressible flows. Furthermore, we show the operator inference performance in learning low-order models using two benchmark problems and compare with an intrusive method, namely proper orthogonal decomposition, and other data-driven approaches.