Active Sampling of Interpolation Points to Identify Dominant Subspaces for Model Reduction

Model reduction is an active research field to construct low-dimensional surrogate models of high fidelity to accelerate engineering design cycles. In this work, we investigate model reduction for linear structured systems using dominant reachable and observable subspaces. When the training set $-$ containing all possible interpolation points $-$ is large, then these subspaces can be determined by solving many large-scale linear systems. However, for high-fidelity models, this easily becomes computationally intractable. To circumvent this issue, in this work, we propose an active sampling strategy to sample only a few points from the given training set, which can allow us to estimate those subspaces accurately. To this end, we formulate the identification of the subspaces as the solution of the generalized Sylvester equations, guiding us to select the most relevant samples from the training set to achieve our goals. Consequently, we construct solutions of the matrix equations in low-rank forms, which encode subspace information. We extensively discuss computational aspects and efficient usage of the low-rank factors in the process of obtaining reduced-order models. We illustrate the proposed active sampling scheme to obtain reduced-order models via dominant reachable and observable subspaces and present its comparison with the method where all the points from the training set are taken into account. It is shown that the active sample strategy can provide us $17$x speed-up without sacrificing any noticeable accuracy.

Stability-Certified Learning of Control Systems with Quadratic Nonlinearities

This work primarily focuses on an operator inference methodology aimed at constructing low-dimensional dynamical models based on a priori hypotheses about their structure, often informed by established physics or expert insights. Stability is a fundamental attribute of dynamical systems, yet it is not always assured in models derived through inference. Our main objective is to develop a method that facilitates the inference of quadratic control dynamical systems with inherent stability guarantees. To this aim, we investigate the stability characteristics of control systems with energy-preserving nonlinearities, thereby identifying conditions under which such systems are bounded-input bounded-state stable. These insights are subsequently applied to the learning process, yielding inferred models that are inherently stable by design. The efficacy of our proposed framework is demonstrated through a couple of numerical examples.

Guaranteed Stable Quadratic Models and their applications in SINDy and Operator Inference

Scientific machine learning for learning dynamical systems is a powerful tool that combines data-driven modeling models, physics-based modeling, and empirical knowledge. It plays an essential role in an engineering design cycle and digital twinning. In this work, we primarily focus on an operator inference methodology that builds dynamical models, preferably in low-dimension, with a prior hypothesis on the model structure, often determined by known physics or given by experts. Then, for inference, we aim to learn the operators of a model by setting up an appropriate optimization problem. One of the critical properties of dynamical systems is{stability. However, such a property is not guaranteed by the inferred models. In this work, we propose inference formulations to learn quadratic models, which are stable by design. Precisely, we discuss the parameterization of quadratic systems that are locally and globally stable. Moreover, for quadratic systems with no stable point yet bounded (e.g., Chaotic Lorenz model), we discuss an attractive trapping region philosophy and a parameterization of such systems. Using those parameterizations, we set up inference problems, which are then solved using a gradient-based optimization method. Furthermore, to avoid numerical derivatives and still learn continuous systems, we make use of an integration form of differential equations. We present several numerical examples, illustrating the preservation of stability and discussing its comparison with the existing state-of-the-art approach to infer operators. By means of numerical examples, we also demonstrate how proposed methods are employed to discover governing equations and energy-preserving models.

Inference of Continuous Linear Systems from Data with Guaranteed Stability

Machine-learning technologies for learning dynamical systems from data play an important role in engineering design. This research focuses on learning continuous linear models from data. Stability, a key feature of dynamic systems, is especially important in design tasks such as prediction and control. Thus, there is a need to develop methodologies that provide stability guarantees. To that end, we leverage the parameterization of stable matrices proposed in [Gillis/Sharma, Automatica, 2017] to realize the desired models. Furthermore, to avoid the estimation of derivative information to learn continuous systems, we formulate the inference problem in an integral form. We also discuss a few extensions, including those related to control systems. Numerical experiments show that the combination of a stable matrix parameterization and an integral form of differential equations allows us to learn stable systems without requiring derivative information, which can be challenging to obtain in situations with noisy or limited data.

Operator Inference and Physics-Informed Learning of Low-Dimensional Models for Incompressible Flows

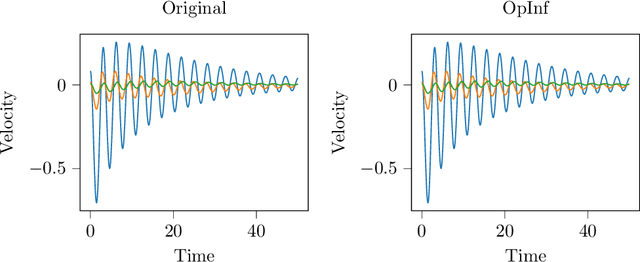
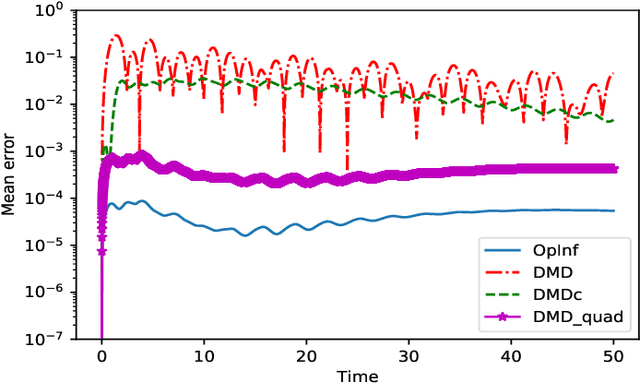
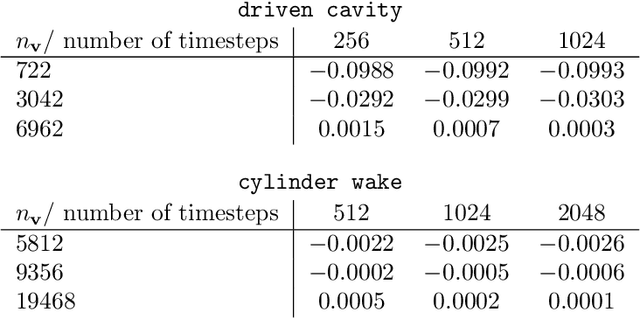
Reduced-order modeling has a long tradition in computational fluid dynamics. The ever-increasing significance of data for the synthesis of low-order models is well reflected in the recent successes of data-driven approaches such as Dynamic Mode Decomposition and Operator Inference. With this work, we suggest a new approach to learning structured low-order models for incompressible flow from data that can be used for engineering studies such as control, optimization, and simulation. To that end, we utilize the intrinsic structure of the Navier-Stokes equations for incompressible flows and show that learning dynamics of the velocity and pressure can be decoupled, thus leading to an efficient operator inference approach for learning the underlying dynamics of incompressible flows. Furthermore, we show the operator inference performance in learning low-order models using two benchmark problems and compare with an intrusive method, namely proper orthogonal decomposition, and other data-driven approaches.