Multi-modal Uncertainty Robust Tree Cover Segmentation For High-Resolution Remote Sensing Images

Recent advances in semantic segmentation of multi-modal remote sensing images have significantly improved the accuracy of tree cover mapping, supporting applications in urban planning, forest monitoring, and ecological assessment. Integrating data from multiple modalities-such as optical imagery, light detection and ranging (LiDAR), and synthetic aperture radar (SAR)-has shown superior performance over single-modality methods. However, these data are often acquired days or even months apart, during which various changes may occur, such as vegetation disturbances (e.g., logging, and wildfires) and variations in imaging quality. Such temporal misalignments introduce cross-modal uncertainty, especially in high-resolution imagery, which can severely degrade segmentation accuracy. To address this challenge, we propose MURTreeFormer, a novel multi-modal segmentation framework that mitigates and leverages aleatoric uncertainty for robust tree cover mapping. MURTreeFormer treats one modality as primary and others as auxiliary, explicitly modeling patch-level uncertainty in the auxiliary modalities via a probabilistic latent representation. Uncertain patches are identified and reconstructed from the primary modality's distribution through a VAE-based resampling mechanism, producing enhanced auxiliary features for fusion. In the decoder, a gradient magnitude attention (GMA) module and a lightweight refinement head (RH) are further integrated to guide attention toward tree-like structures and to preserve fine-grained spatial details. Extensive experiments on multi-modal datasets from Shanghai and Zurich demonstrate that MURTreeFormer significantly improves segmentation performance and effectively reduces the impact of temporally induced aleatoric uncertainty.

A Generalized Tensor Formulation for Hyperspectral Image Super-Resolution Under General Spatial Blurring

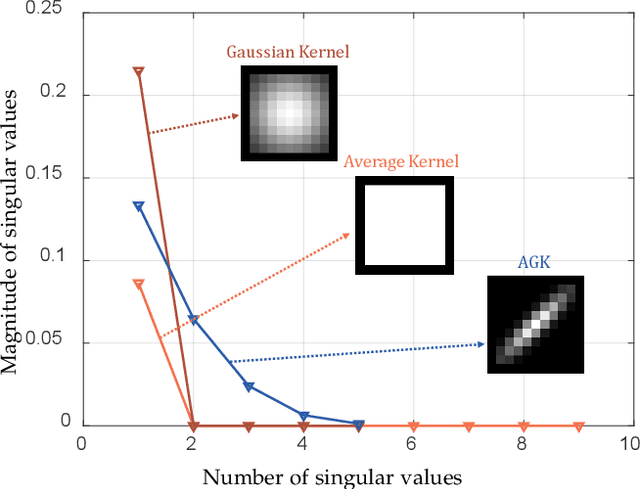
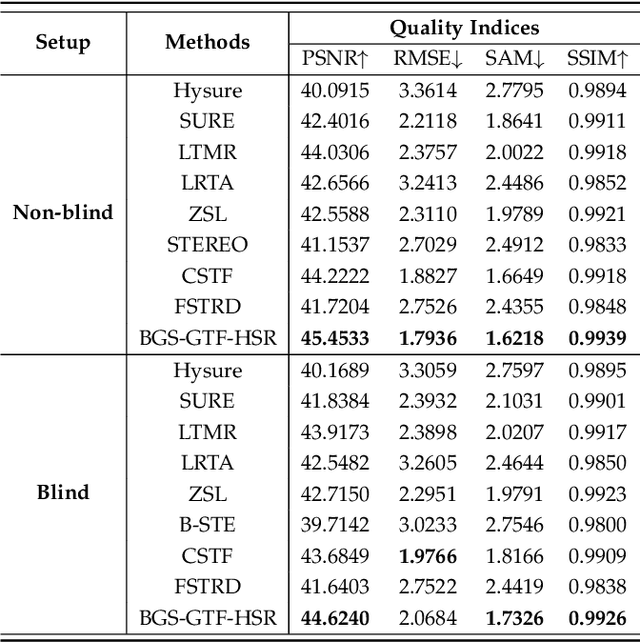
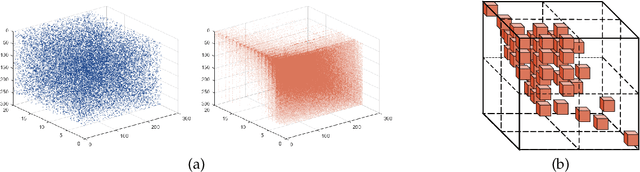
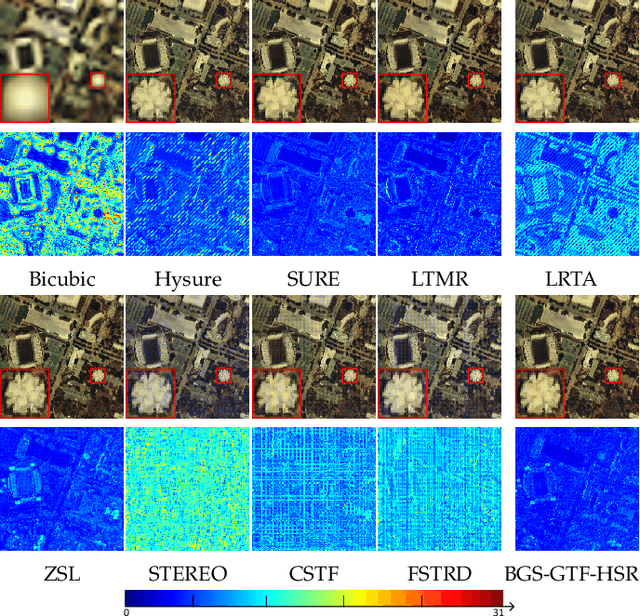
Hyperspectral super-resolution is commonly accomplished by the fusing of a hyperspectral imaging of low spatial resolution with a multispectral image of high spatial resolution, and many tensor-based approaches to this task have been recently proposed. Yet, it is assumed in such tensor-based methods that the spatial-blurring operation that creates the observed hyperspectral image from the desired super-resolved image is separable into independent horizontal and vertical blurring. Recent work has argued that such separable spatial degradation is ill-equipped to model the operation of real sensors which may exhibit, for example, anisotropic blurring. To accommodate this fact, a generalized tensor formulation based on a Kronecker decomposition is proposed to handle any general spatial-degradation matrix, including those that are not separable as previously assumed. Analysis of the generalized formulation reveals conditions under which exact recovery of the desired super-resolved image is guaranteed, and a practical algorithm for such recovery, driven by a blockwise-group-sparsity regularization, is proposed. Extensive experimental results demonstrate that the proposed generalized tensor approach outperforms not only traditional matrix-based techniques but also state-of-the-art tensor-based methods; the gains with respect to the latter are especially significant in cases of anisotropic spatial blurring.

A Survey on Hyperspectral Image Restoration: From the View of Low-Rank Tensor Approximation

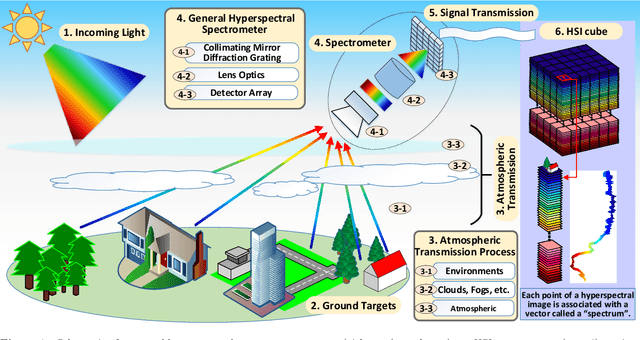
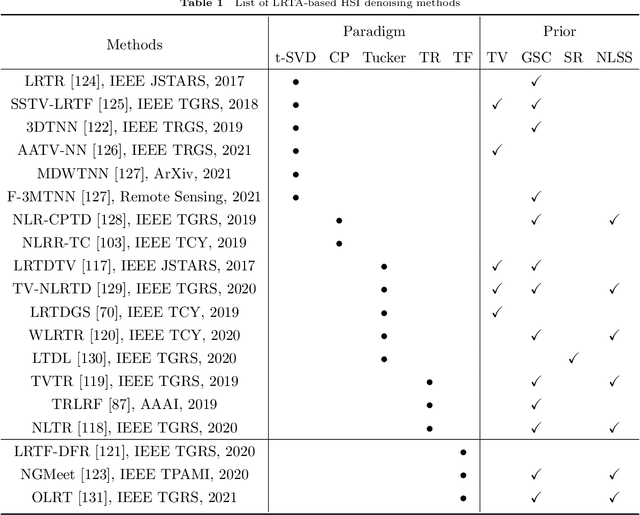
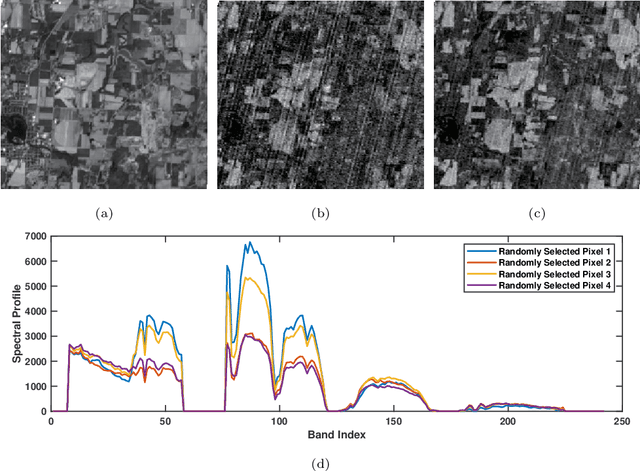
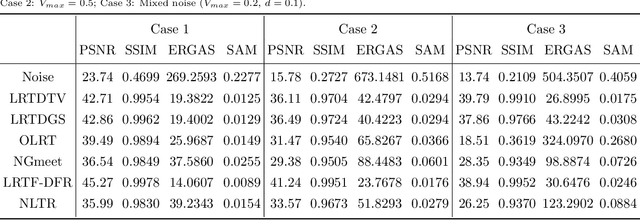
The ability of capturing fine spectral discriminative information enables hyperspectral images (HSIs) to observe, detect and identify objects with subtle spectral discrepancy. However, the captured HSIs may not represent true distribution of ground objects and the received reflectance at imaging instruments may be degraded, owing to environmental disturbances, atmospheric effects and sensors' hardware limitations. These degradations include but are not limited to: complex noise (i.e., Gaussian noise, impulse noise, sparse stripes, and their mixtures), heavy stripes, deadlines, cloud and shadow occlusion, blurring and spatial-resolution degradation and spectral absorption, etc. These degradations dramatically reduce the quality and usefulness of HSIs. Low-rank tensor approximation (LRTA) is such an emerging technique, having gained much attention in HSI restoration community, with ever-growing theoretical foundation and pivotal technological innovation. Compared to low-rank matrix approximation (LRMA), LRTA is capable of characterizing more complex intrinsic structure of high-order data and owns more efficient learning abilities, being established to address convex and non-convex inverse optimization problems induced by HSI restoration. This survey mainly attempts to present a sophisticated, cutting-edge, and comprehensive technical survey of LRTA toward HSI restoration, specifically focusing on the following six topics: Denoising, Destriping, Inpainting, Deblurring, Super--resolution and Fusion. The theoretical development and variants of LRTA techniques are also elaborated. For each topic, the state-of-the-art restoration methods are compared by assessing their performance both quantitatively and visually. Open issues and challenges are also presented, including model formulation, algorithm design, prior exploration and application concerning the interpretation requirements.