Interaction Pursuit with Feature Screening and Selection

Understanding how features interact with each other is of paramount importance in many scientific discoveries and contemporary applications. Yet interaction identification becomes challenging even for a moderate number of covariates. In this paper, we suggest an efficient and flexible procedure, called the interaction pursuit (IP), for interaction identification in ultra-high dimensions. The suggested method first reduces the number of interactions and main effects to a moderate scale by a new feature screening approach, and then selects important interactions and main effects in the reduced feature space using regularization methods. Compared to existing approaches, our method screens interactions separately from main effects and thus can be more effective in interaction screening. Under a fairly general framework, we establish that for both interactions and main effects, the method enjoys the sure screening property in screening and oracle inequalities in selection. Our method and theoretical results are supported by several simulation and real data examples.

Interaction pursuit in high-dimensional multi-response regression via distance correlation

Feature interactions can contribute to a large proportion of variation in many prediction models. In the era of big data, the coexistence of high dimensionality in both responses and covariates poses unprecedented challenges in identifying important interactions. In this paper, we suggest a two-stage interaction identification method, called the interaction pursuit via distance correlation (IPDC), in the setting of high-dimensional multi-response interaction models that exploits feature screening applied to transformed variables with distance correlation followed by feature selection. Such a procedure is computationally efficient, generally applicable beyond the heredity assumption, and effective even when the number of responses diverges with the sample size. Under mild regularity conditions, we show that this method enjoys nice theoretical properties including the sure screening property, support union recovery, and oracle inequalities in prediction and estimation for both interactions and main effects. The advantages of our method are supported by several simulation studies and real data analysis.

The constrained Dantzig selector with enhanced consistency

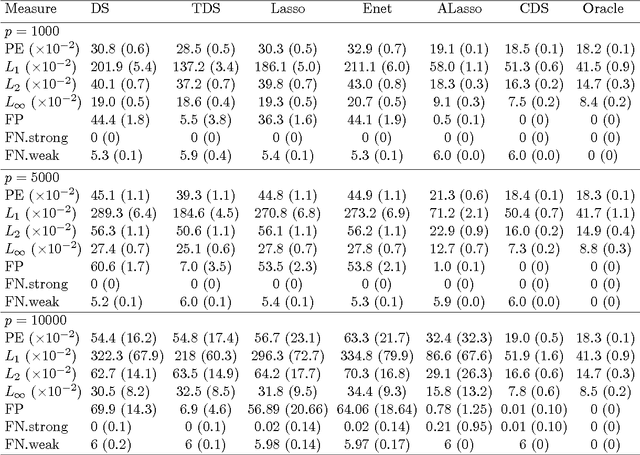
The Dantzig selector has received popularity for many applications such as compressed sensing and sparse modeling, thanks to its computational efficiency as a linear programming problem and its nice sampling properties. Existing results show that it can recover sparse signals mimicking the accuracy of the ideal procedure, up to a logarithmic factor of the dimensionality. Such a factor has been shown to hold for many regularization methods. An important question is whether this factor can be reduced to a logarithmic factor of the sample size in ultra-high dimensions under mild regularity conditions. To provide an affirmative answer, in this paper we suggest the constrained Dantzig selector, which has more flexible constraints and parameter space. We prove that the suggested method can achieve convergence rates within a logarithmic factor of the sample size of the oracle rates and improved sparsity, under a fairly weak assumption on the signal strength. Such improvement is significant in ultra-high dimensions. This method can be implemented efficiently through sequential linear programming. Numerical studies confirm that the sample size needed for a certain level of accuracy in these problems can be much reduced.

Innovated interaction screening for high-dimensional nonlinear classification

This paper is concerned with the problems of interaction screening and nonlinear classification in a high-dimensional setting. We propose a two-step procedure, IIS-SQDA, where in the first step an innovated interaction screening (IIS) approach based on transforming the original $p$-dimensional feature vector is proposed, and in the second step a sparse quadratic discriminant analysis (SQDA) is proposed for further selecting important interactions and main effects and simultaneously conducting classification. Our IIS approach screens important interactions by examining only $p$ features instead of all two-way interactions of order $O(p^2)$. Our theory shows that the proposed method enjoys sure screening property in interaction selection in the high-dimensional setting of $p$ growing exponentially with the sample size. In the selection and classification step, we establish a sparse inequality on the estimated coefficient vector for QDA and prove that the classification error of our procedure can be upper-bounded by the oracle classification error plus some smaller order term. Extensive simulation studies and real data analysis show that our proposal compares favorably with existing methods in interaction selection and high-dimensional classification.