The constrained Dantzig selector with enhanced consistency

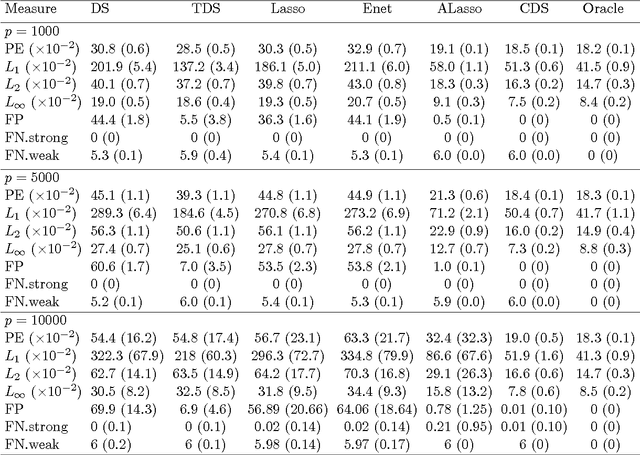
The Dantzig selector has received popularity for many applications such as compressed sensing and sparse modeling, thanks to its computational efficiency as a linear programming problem and its nice sampling properties. Existing results show that it can recover sparse signals mimicking the accuracy of the ideal procedure, up to a logarithmic factor of the dimensionality. Such a factor has been shown to hold for many regularization methods. An important question is whether this factor can be reduced to a logarithmic factor of the sample size in ultra-high dimensions under mild regularity conditions. To provide an affirmative answer, in this paper we suggest the constrained Dantzig selector, which has more flexible constraints and parameter space. We prove that the suggested method can achieve convergence rates within a logarithmic factor of the sample size of the oracle rates and improved sparsity, under a fairly weak assumption on the signal strength. Such improvement is significant in ultra-high dimensions. This method can be implemented efficiently through sequential linear programming. Numerical studies confirm that the sample size needed for a certain level of accuracy in these problems can be much reduced.