CARMI: A Cache-Aware Learned Index with a Cost-based Construction Algorithm

Learned indexes, which use machine learning models to replace traditional index structures, have shown promising results in recent studies. However, our understanding of this new type of index structure is still at an early stage with many details that need to be carefully examined and improved. In this paper, we propose a cache-aware learned index (CARMI) design to improve the efficiency of the Recursive Model Index (RMI) framework proposed by Kraska et al. and a cost-based construction algorithm to construct the optimal indexes in a wide variety of application scenarios. We formulate the problem of finding the optimal design of a learned index as an optimization problem and propose a dynamic programming algorithm for solving it and a partial greedy step to speed up. Experiments show that our index construction strategy can construct indexes with significantly better performance compared to baselines under various data distribution and workload requirements. Among them, CARMI can obtain an average of 2.52X speedup compared to B-tree, while using only about 0.56X memory space of B-tree on average.

The Importance of Norm Regularization in Linear Graph Embedding: Theoretical Analysis and Empirical Demonstration

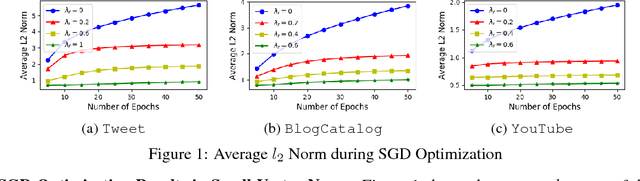
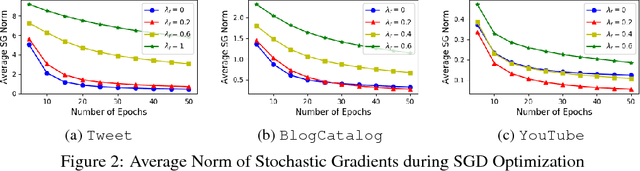
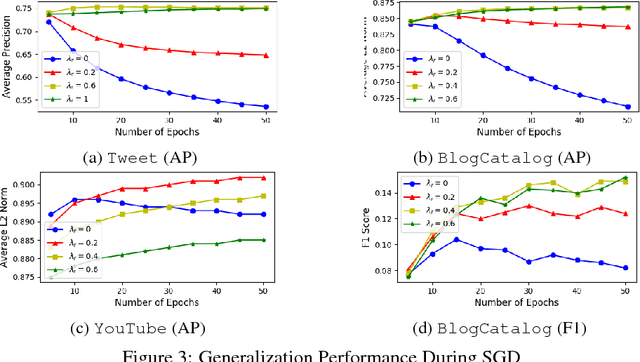
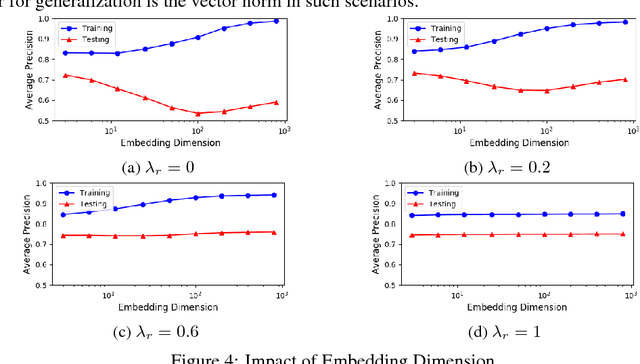
Learning distributed representations for nodes in graphs is a crucial primitive in network analysis with a wide spectrum of applications. Linear graph embedding methods learn such representations by optimizing the likelihood of both positive and negative edges while constraining the dimension of the embedding vectors. We argue that the generalization performance of these methods is not due to the dimensionality constraint as commonly believed, but rather the small norm of embedding vectors. Both theoretical and empirical evidence are provided to support this argument: (a) we prove that the generalization error of these methods can be bounded by limiting the norm of vectors, regardless of the embedding dimension; (b) we show that the generalization performance of linear graph embedding methods is correlated with the norm of embedding vectors, which is small due to the early stopping of SGD and the vanishing gradients. We performed extensive experiments to validate our analysis and showcased the importance of proper norm regularization in practice.

On the Interpretability of Conditional Probability Estimates in the Agnostic Setting

We study the interpretability of conditional probability estimates for binary classification under the agnostic setting or scenario. Under the agnostic setting, conditional probability estimates do not necessarily reflect the true conditional probabilities. Instead, they have a certain calibration property: among all data points that the classifier has predicted P(Y = 1|X) = p, p portion of them actually have label Y = 1. For cost-sensitive decision problems, this calibration property provides adequate support for us to use Bayes Decision Theory. In this paper, we define a novel measure for the calibration property together with its empirical counterpart, and prove an uniform convergence result between them. This new measure enables us to formally justify the calibration property of conditional probability estimations, and provides new insights on the problem of estimating and calibrating conditional probabilities.