The Importance of Norm Regularization in Linear Graph Embedding: Theoretical Analysis and Empirical Demonstration

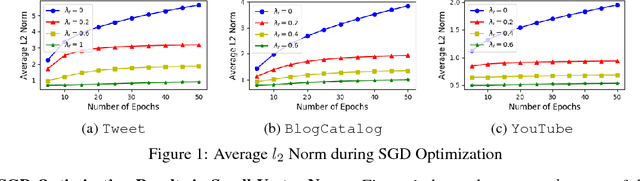
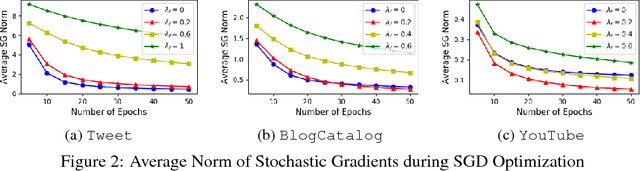
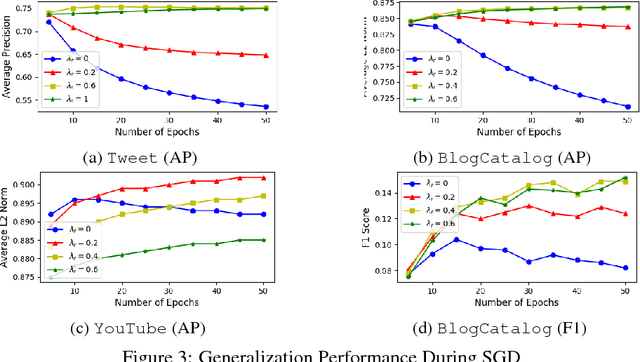
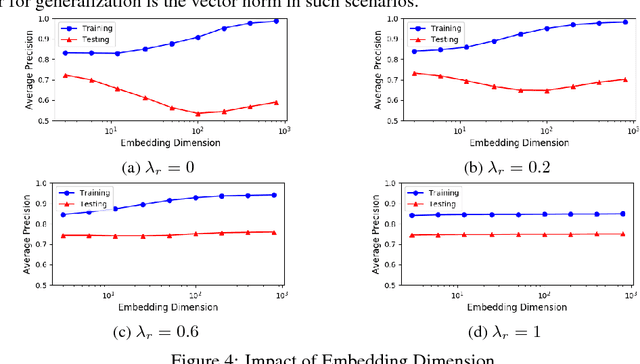
Learning distributed representations for nodes in graphs is a crucial primitive in network analysis with a wide spectrum of applications. Linear graph embedding methods learn such representations by optimizing the likelihood of both positive and negative edges while constraining the dimension of the embedding vectors. We argue that the generalization performance of these methods is not due to the dimensionality constraint as commonly believed, but rather the small norm of embedding vectors. Both theoretical and empirical evidence are provided to support this argument: (a) we prove that the generalization error of these methods can be bounded by limiting the norm of vectors, regardless of the embedding dimension; (b) we show that the generalization performance of linear graph embedding methods is correlated with the norm of embedding vectors, which is small due to the early stopping of SGD and the vanishing gradients. We performed extensive experiments to validate our analysis and showcased the importance of proper norm regularization in practice.